https://www.acmicpc.net/problem/17611
17611번: 직각다각형
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지는 꼭지점들의 순서는 시계방향이다. 다각형의 꼭지점을 나타내는 각 좌표값은 정수이며, -500,000 ≤ xi, yi ≤ 500,000이다.
www.acmicpc.net
문제
다각형의 두 선분이 연속하는 선분의 꼭짓점을 제외하고는 만나지 않는 다각형을 단순다각형이라고 부른다. 다각형의 각 변이 x축과 y축에 평행한 다각형을 직각다각형이라 부른다. 단순다각형이면서 직각다각형을 단순직각다각형이라 부른다. 아래 두 그림은 단순직각다각형의 예를 보여준다.
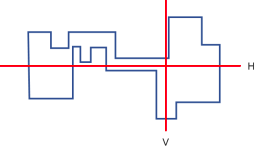
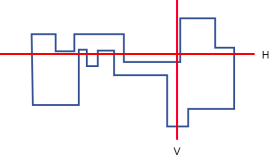
단순직각다각형이 주어질 때, 수평선 H가 다각형의 수직선분과 몇 번 교차하는지 또는 수직선 V가 다각형의 수평선분과 몇 번 교차하는지 알고자 한다. 첫 번째 그림에서 수평선 H는 4개의 수직선분과 교차하고 수직선 V는 2개의 수평선분과 교차한다. 두 번째 그림은 첫 번째 그림에서 수평선 H의 위치를 조금 위로 옮긴 것으로 8개의 수직선분과 교차하게 된다.
이때, 단순직각다각형과 가장 많이 교차하는 수평선 H와 수직선 V의 위치를 찾아 그때의 교차 횟수를 구하고자 한다. 단, 수평선 H는 다각형의 어떤 수평선분과도 겹처 놓여서는 안 되고, 유사하게 수직선 V는 다각형의 어떤 수직선분과도 겹쳐 놓여서는 안 된다.
수평선 H의 위치를 잘 정해서 주어진 단순직각다각형의 수직선분과 가장 많이 교차하는 지점을 찾을 때, 그 때의 교차 횟수를 h라 하고, 유사하게 수직선 V와 주어진 단순직각다각형의 수평선분과 가장 많이 교차하는 횟수를 v라 할 때, max(h, v)를 출력하는 프로그램을 작성하시오.
입력
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지는 꼭지점들의 순서는 시계방향이다. 다각형의 꼭지점을 나타내는 각 좌표값은 정수이며, -500,000 ≤ xi, yi ≤ 500,000이다.
출력
max(h, v)를 출력한다.
***************************************************************
문제 지문읽는 난이도가 수능 비문학 지문읽는것 같습니다. 이럴땐 입력과 출력, 그리고 예제로 문제의 설명을 이해해야합니다. 예제를 따라 그림을 그리면 이제 뭔가 문제의 윤곽이 잡히는 것 같습니다. 수평선 또는 수직선을 적절히 도형의 선분과 겹치지 않게 놓은 경우의 수 중 가장 도형과 많이 접한 점의 개수를 구해야합니다.
*풀이에 앞서 이 문제의 의도와 정해는 적절한 정렬을 거친 라인스위핑 문제입니다. 저는 다른 방식으로 풀었지만 라인스위핑 편이 훨씬 퍼포먼스가 좋습니다. 저의 풀이는 이런 풀이가 있구나 하는 참고로만 보셨으면 좋겠습니다.*
주어진 좌표를 따라 도형을 만들어가다 보면 다음과 같은 특이한 점을 발견할 수 있습니다.
만약 가로로 줄을 그었고, 그 범위에 수직선을 놓는다면 도형과 접한 점의 개수가 1개 늘어나게 되고,
세로로 줄을 그었고, 그 범위에 수평선을 놓는다면 마찬가지로 도형과 접한 점의 개수가 1개 늘어나게 됩니다.
문제를 이렇게 다르게 해석해 볼 수도 있지 않을까요?
주어진 꼭짓점들의 좌표를 입력받아 가로, 혹은 세로로 줄을 긋는데, 가로로 줄을 그었다면 그 범위의 수직선을 그었을때 도형과 접한 점의 개수를 1 추가해주고, 세로는 그 반대로 한다.
->수평선과 수직선. 2개의 세그먼트 트리를 만들고 꼭짓점들의 좌표 수 만큼의 쿼리의 내용이 left~right만큼의 범위에 1을 추가를 해야하는 내용일때, 적절한 자료구조 및 알고리즘은 무엇일까?
답은 lazy propagation 입니다. 꼭짓점들의 좌표를 받아 직선을 긋는데, 만약 가로선을 그었다면 (x1+1,x2)범위의 수직선 세그먼트 트리에 1을 추가해주고, 세로선을 그었다면 (y1+1,y2)범위의 수평선 세그먼트 트리에 1을 추가해주면 됩니다.
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <vector>
using namespace std;
typedef long long ll;
const int INF=987654321,MAX_N=500000+2;
int N;
vector<pair<int,int>>v;
struct SEG_TREE
{
int n;
vector <int> tree,lazy;
SEG_TREE(){;};
SEG_TREE(int len)
{
n=len;
tree.resize(n*4,0),lazy.resize(n*4,0);
}
void propagate(int nodeLeft,int nodeRight,int node)
{
if(lazy[node])
{
if(nodeLeft!=nodeRight)
{
lazy[node*2]+=lazy[node];
lazy[node*2+1]+=lazy[node];
}
tree[node]+=lazy[node]*(nodeRight-nodeLeft+1);
lazy[node]=0;
}
}
int update(int left,int right,int value)
{
return update(left,right,value,0,n-1,1);
}
int update(const int left,const int right,const int value,int nodeLeft,int nodeRight,int node)
{
propagate(nodeLeft,nodeRight,node);
if(nodeRight<left||right<nodeLeft) return tree[node];
if(left<=nodeLeft&&nodeRight<=right)
{
lazy[node]+=value;
propagate(nodeLeft,nodeRight,node);
return tree[node];
}
int mid=(nodeLeft+nodeRight)/2;
return tree[node]=update(left,right,value,nodeLeft,mid,node*2)+
update(left,right,value,mid+1,nodeRight,node*2+1);
}
int query(int left,int right)
{
return query(left,right,0,n-1,1);
}
int query(const int left,const int right,int nodeLeft,int nodeRight,int node)
{
propagate(nodeLeft,nodeRight,node);
if(nodeRight<left||right<nodeLeft) return 0;
if(left<=nodeLeft&&nodeRight<=right) return tree[node];
int mid=(nodeLeft+nodeRight)/2;
return query(left,right,nodeLeft,mid,node*2)+
query(left,right,mid+1,nodeRight,node*2+1);
}
};
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin>>N;
SEG_TREE segY(MAX_N*2),segX(MAX_N*2);
for(int i=0;i<N;i++)
{
int y,x;
cin>>y>>x;
v.push_back({y,x});
}
v.push_back(v[0]);
for(int i=1;i<=N;i++)
{
if(v[i].first==v[i-1].first)
segX.update(min(v[i-1].second,v[i].second)+1+MAX_N,
max(v[i-1].second,v[i].second)+MAX_N,1);
else
segY.update(min(v[i-1].first,v[i].first)+1+MAX_N,
max(v[i-1].first,v[i].first)+MAX_N,1);
}
int ans=0;
for(int i=-MAX_N;i<MAX_N;i++)
ans=max(ans,(int)max(segY.query(i+MAX_N,i+MAX_N),segX.query(i+MAX_N,i+MAX_N)));
cout<<ans;
}
주어진 마지막 꼭짓점에서 처음 시작점까지도 직선을 그어야하므로 v.push_back(v[0])을 사용했습니다.
또한 좌표의 범위가 -500,000 ≤ xi, yi ≤ 500,000 의 음수값도 포함이 되므로 모든좌표에 MAX_N을 추가를하여 구현했습니다. 그리고 세그먼트 트리를 업데이트 할때의 범위는 (x1~x2)가 아니라 (x1+1,~x2)가 되어야 합니다. off-by-one오류를 범하지 않게 조심해야합니다.
지문 해석의 난이도와 그림에 나오는 도형의 압박감에 잠깐 클릭만했다가 포기하는 분들이 많을 것 같은 문제입니다.
물론 저도 대회에 이런 문제가 나왔다면 제껴두고 다른 문제를 먼저 풀것같긴 합니다..
'📌BOJ 알고리즘 트레이닝' 카테고리의 다른 글
| [BOJ][백준]그리디 알고리즘-17609번 회문 (0) | 2019.11.15 |
|---|---|
| [BOJ][백준]그리디 알고리즘-17615번 볼 모으기 (0) | 2019.10.15 |
| [BOJ][백준]브루트 포스-17610번 양팔저울 (0) | 2019.10.13 |
| [BOJ][백준]DP-17528번 Two Machines (0) | 2019.10.10 |
| [BOJ][백준]Simulation-17135번 캐슬 디팬스 (0) | 2019.04.11 |
https://www.acmicpc.net/problem/17611
17611번: 직각다각형
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지는 꼭지점들의 순서는 시계방향이다. 다각형의 꼭지점을 나타내는 각 좌표값은 정수이며, -500,000 ≤ xi, yi ≤ 500,000이다.
www.acmicpc.net
문제
다각형의 두 선분이 연속하는 선분의 꼭짓점을 제외하고는 만나지 않는 다각형을 단순다각형이라고 부른다. 다각형의 각 변이 x축과 y축에 평행한 다각형을 직각다각형이라 부른다. 단순다각형이면서 직각다각형을 단순직각다각형이라 부른다. 아래 두 그림은 단순직각다각형의 예를 보여준다.


단순직각다각형이 주어질 때, 수평선 H가 다각형의 수직선분과 몇 번 교차하는지 또는 수직선 V가 다각형의 수평선분과 몇 번 교차하는지 알고자 한다. 첫 번째 그림에서 수평선 H는 4개의 수직선분과 교차하고 수직선 V는 2개의 수평선분과 교차한다. 두 번째 그림은 첫 번째 그림에서 수평선 H의 위치를 조금 위로 옮긴 것으로 8개의 수직선분과 교차하게 된다.
이때, 단순직각다각형과 가장 많이 교차하는 수평선 H와 수직선 V의 위치를 찾아 그때의 교차 횟수를 구하고자 한다. 단, 수평선 H는 다각형의 어떤 수평선분과도 겹처 놓여서는 안 되고, 유사하게 수직선 V는 다각형의 어떤 수직선분과도 겹쳐 놓여서는 안 된다.
수평선 H의 위치를 잘 정해서 주어진 단순직각다각형의 수직선분과 가장 많이 교차하는 지점을 찾을 때, 그 때의 교차 횟수를 h라 하고, 유사하게 수직선 V와 주어진 단순직각다각형의 수평선분과 가장 많이 교차하는 횟수를 v라 할 때, max(h, v)를 출력하는 프로그램을 작성하시오.
입력
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지는 꼭지점들의 순서는 시계방향이다. 다각형의 꼭지점을 나타내는 각 좌표값은 정수이며, -500,000 ≤ xi, yi ≤ 500,000이다.
출력
max(h, v)를 출력한다.
***************************************************************
문제 지문읽는 난이도가 수능 비문학 지문읽는것 같습니다. 이럴땐 입력과 출력, 그리고 예제로 문제의 설명을 이해해야합니다. 예제를 따라 그림을 그리면 이제 뭔가 문제의 윤곽이 잡히는 것 같습니다. 수평선 또는 수직선을 적절히 도형의 선분과 겹치지 않게 놓은 경우의 수 중 가장 도형과 많이 접한 점의 개수를 구해야합니다.
*풀이에 앞서 이 문제의 의도와 정해는 적절한 정렬을 거친 라인스위핑 문제입니다. 저는 다른 방식으로 풀었지만 라인스위핑 편이 훨씬 퍼포먼스가 좋습니다. 저의 풀이는 이런 풀이가 있구나 하는 참고로만 보셨으면 좋겠습니다.*
주어진 좌표를 따라 도형을 만들어가다 보면 다음과 같은 특이한 점을 발견할 수 있습니다.
만약 가로로 줄을 그었고, 그 범위에 수직선을 놓는다면 도형과 접한 점의 개수가 1개 늘어나게 되고,
세로로 줄을 그었고, 그 범위에 수평선을 놓는다면 마찬가지로 도형과 접한 점의 개수가 1개 늘어나게 됩니다.
문제를 이렇게 다르게 해석해 볼 수도 있지 않을까요?
주어진 꼭짓점들의 좌표를 입력받아 가로, 혹은 세로로 줄을 긋는데, 가로로 줄을 그었다면 그 범위의 수직선을 그었을때 도형과 접한 점의 개수를 1 추가해주고, 세로는 그 반대로 한다.
->수평선과 수직선. 2개의 세그먼트 트리를 만들고 꼭짓점들의 좌표 수 만큼의 쿼리의 내용이 left~right만큼의 범위에 1을 추가를 해야하는 내용일때, 적절한 자료구조 및 알고리즘은 무엇일까?
답은 lazy propagation 입니다. 꼭짓점들의 좌표를 받아 직선을 긋는데, 만약 가로선을 그었다면 (x1+1,x2)범위의 수직선 세그먼트 트리에 1을 추가해주고, 세로선을 그었다면 (y1+1,y2)범위의 수평선 세그먼트 트리에 1을 추가해주면 됩니다.
#include <iostream>
#include <string>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <vector>
using namespace std;
typedef long long ll;
const int INF=987654321,MAX_N=500000+2;
int N;
vector<pair<int,int>>v;
struct SEG_TREE
{
int n;
vector <int> tree,lazy;
SEG_TREE(){;};
SEG_TREE(int len)
{
n=len;
tree.resize(n*4,0),lazy.resize(n*4,0);
}
void propagate(int nodeLeft,int nodeRight,int node)
{
if(lazy[node])
{
if(nodeLeft!=nodeRight)
{
lazy[node*2]+=lazy[node];
lazy[node*2+1]+=lazy[node];
}
tree[node]+=lazy[node]*(nodeRight-nodeLeft+1);
lazy[node]=0;
}
}
int update(int left,int right,int value)
{
return update(left,right,value,0,n-1,1);
}
int update(const int left,const int right,const int value,int nodeLeft,int nodeRight,int node)
{
propagate(nodeLeft,nodeRight,node);
if(nodeRight<left||right<nodeLeft) return tree[node];
if(left<=nodeLeft&&nodeRight<=right)
{
lazy[node]+=value;
propagate(nodeLeft,nodeRight,node);
return tree[node];
}
int mid=(nodeLeft+nodeRight)/2;
return tree[node]=update(left,right,value,nodeLeft,mid,node*2)+
update(left,right,value,mid+1,nodeRight,node*2+1);
}
int query(int left,int right)
{
return query(left,right,0,n-1,1);
}
int query(const int left,const int right,int nodeLeft,int nodeRight,int node)
{
propagate(nodeLeft,nodeRight,node);
if(nodeRight<left||right<nodeLeft) return 0;
if(left<=nodeLeft&&nodeRight<=right) return tree[node];
int mid=(nodeLeft+nodeRight)/2;
return query(left,right,nodeLeft,mid,node*2)+
query(left,right,mid+1,nodeRight,node*2+1);
}
};
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin>>N;
SEG_TREE segY(MAX_N*2),segX(MAX_N*2);
for(int i=0;i<N;i++)
{
int y,x;
cin>>y>>x;
v.push_back({y,x});
}
v.push_back(v[0]);
for(int i=1;i<=N;i++)
{
if(v[i].first==v[i-1].first)
segX.update(min(v[i-1].second,v[i].second)+1+MAX_N,
max(v[i-1].second,v[i].second)+MAX_N,1);
else
segY.update(min(v[i-1].first,v[i].first)+1+MAX_N,
max(v[i-1].first,v[i].first)+MAX_N,1);
}
int ans=0;
for(int i=-MAX_N;i<MAX_N;i++)
ans=max(ans,(int)max(segY.query(i+MAX_N,i+MAX_N),segX.query(i+MAX_N,i+MAX_N)));
cout<<ans;
}
주어진 마지막 꼭짓점에서 처음 시작점까지도 직선을 그어야하므로 v.push_back(v[0])을 사용했습니다.
또한 좌표의 범위가 -500,000 ≤ xi, yi ≤ 500,000 의 음수값도 포함이 되므로 모든좌표에 MAX_N을 추가를하여 구현했습니다. 그리고 세그먼트 트리를 업데이트 할때의 범위는 (x1~x2)가 아니라 (x1+1,~x2)가 되어야 합니다. off-by-one오류를 범하지 않게 조심해야합니다.
지문 해석의 난이도와 그림에 나오는 도형의 압박감에 잠깐 클릭만했다가 포기하는 분들이 많을 것 같은 문제입니다.
물론 저도 대회에 이런 문제가 나왔다면 제껴두고 다른 문제를 먼저 풀것같긴 합니다..
'📌BOJ 알고리즘 트레이닝' 카테고리의 다른 글
| [BOJ][백준]그리디 알고리즘-17609번 회문 (0) | 2019.11.15 |
|---|---|
| [BOJ][백준]그리디 알고리즘-17615번 볼 모으기 (0) | 2019.10.15 |
| [BOJ][백준]브루트 포스-17610번 양팔저울 (0) | 2019.10.13 |
| [BOJ][백준]DP-17528번 Two Machines (0) | 2019.10.10 |
| [BOJ][백준]Simulation-17135번 캐슬 디팬스 (0) | 2019.04.11 |