https://www.acmicpc.net/problem/17528
17528번: Two Machines
문제 스케줄링 최적화 회사인 SOPT 에 완료해야 할 n개의 작업 t1, t2, ..., tn 이 있다. SOPT 회사는 두 대의 머신 A 와 B 를 보유하고 있다. 각 작업 ti를 완료하기 위해 SOPT 는 머신 A 와 B 둘 중에 오직 하나를 선택할 수 있다. 작업 ti를 완료하기 위해 머신 A를 선택하면 ai시간이 걸리고 머신 B를 선택하면 bi 시간이 걸린다. 각 머신은 어느 순간에 최대 하나의 작업만 수행할 수 있으며, 한 작업이 시작되면 그 작
www.acmicpc.net
문제
스케줄링 최적화 회사인 SOPT 에 완료해야 할 n개의 작업 t1, t2, ..., tn 이 있다. SOPT 회사는 두 대의 머신 A 와 B 를 보유하고 있다. 각 작업 ti를 완료하기 위해 SOPT 는 머신 A 와 B 둘 중에 오직 하나를 선택할 수 있다. 작업 ti를 완료하기 위해 머신 A를 선택하면 ai시간이 걸리고 머신 B를 선택하면 bi 시간이 걸린다. 각 머신은 어느 순간에 최대 하나의 작업만 수행할 수 있으며, 한 작업이 시작되면 그 작업을 완료하기 전까지 다른 작업을 그 머신에서 수행할 수 없다. SOPT 는 모든 작업을 완료하기 위한 최소의 완료 시간을 구하고자 한다.
예를 들어, 세 개의 작업이 t1, t2, t3가 주어져 있고 a1 = 2, b1 = 3, a2 = 5, b2 = 3, a3 = 2, b3 = 7라고 하자. 완료 시간을 최소화하기 위해서는 작업 t1, t3는 머신 A에, 작업 t2는 머신 B에 할당한다. 머신 A는 작업 t1, t3를 완료하는데 2 + 2 = 4 시간이 걸리고 머신 B는 작업 t2를 완료하는데 3 시간이 걸린다. 따라서 최소 완료 시간은 4 시간이 된다. n개의 작업 t1, t2, ..., tn 과 각 머신에서 각 작업들을 수행하는 데 걸리는 시간들이 주어질 때, 모든 작업들을 완료하기 위해 걸리는 시간의 최솟값을 구하는 프로그램을 작성하시오.
입력
입력은 표준입력을 사용한다. 첫 번째 줄에 작업의 개수를 나타내는 양의 정수 n (1 ≤ n ≤ 250)이 주어진다. 다음 n개의 줄에서 i번째 줄에는 두 개의 정수 ai, bi (1 ≤ ai, bi ≤ 250)가 주어진다. 여기서 ai와 bi는 각각 작업 ti를 머신 A와 B에서 완료하는데 걸리는 시간이다.
출력
출력은 표준출력을 사용한다. 모든 작업 t1, t2, ..., tn을 완료하기 위한 최소의 완료시간을 한 줄에 출력한다.
****************************************************************************************************
참 이상한 문제였습니다. 분명 풀어본 것 같았고, 흔히 말하는 웰노운 문제 같았고, 시간 과 크기 제한도 크지 않은 것 같았습니다. 하지만 몇시간동안 고민한 문제인 two machine문제를 리뷰해보자면,
처음에 직관적으로 생각한 풀이는N^5의 [idx][A머신의 시간할당량][B머신의 시간할당량]풀이였으나 250^5=???
어림도없는 접근이었습니다. 아,근데 이렇게 간단해보이는 문제인데 푼사람은 적고, 정답률은 높으니 (새로운 문제풀때는 solved.ac꺼두고 하는 편입니다.) 풀이가 딴곳으로 샜다는 느낌을 받고 그리디로 접근을 해보았습니다.
생각한 그리디 접근은 2가지였는데,
1)a작업시간 순 정렬,b작업시간 순 정렬 후 최적의 해 구하기
2)|a작업시간-b작업시간|순 정렬 후 최적의 해 구하기
하지만 두가지 전부 이 반례가 존재합니다.
5
10 5
9 4
8 3
7 2
6 1
//answer:10
다시 돌고돌아 dp풀이를 생각했는데, A와B머신의 작업량을 모두 따로 저장해야할 필요가 있을까? 부터 접근을 하여,
[idx][한 머신의 남은 작업량][A머신 or B머신]으로 배열잡기에 성공했습니다.
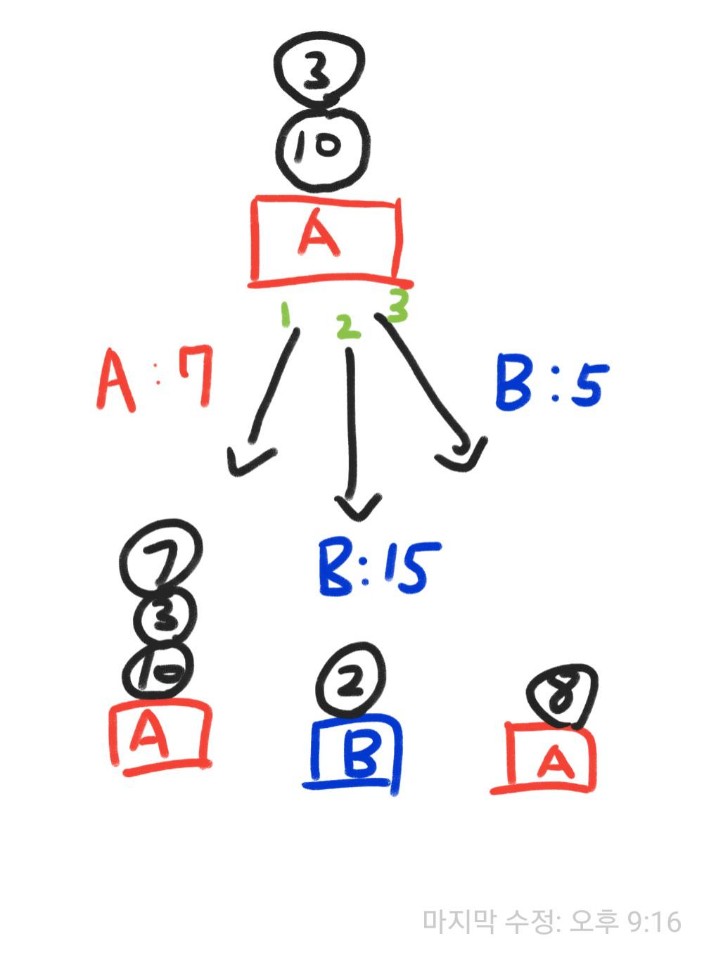
예시로 설명을 해보자면, 먼저 A머신에 13만큼의 작업량이 쌓아져 있다면,
1의경우, A머신에 7만큼의 작업량이 추가되면 그냥 바로 작업량을 추가해 주면됩니다.
2의경우, A머신에 있는 작업량을 초과하는 B의 작업을 수행하려면 A머신에 누적된 작업량을 수행 한 후에,
B머신에 남은 작업량을 할당해줍니다.
3의경우, A머신에 할당된 작업량보다 B의 작업량이 적으므로 B의 작업량만큼 작업을 수행하면 됩니다.
여기서 작업을 수행한다는 말은 시간이 소요된다는 의미로 해석하면 되겠습니다.
수행되는 과정이 lazy propagation이랑 느낌이 비슷하네요.
#include <iostream>
#include <vector>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_N = 250 + 2, INF = 987654321;
int N, cache[MAX_N][MAX_N*MAX_N][2];
vector<pair<int, int>>v;
int f(int idx, int time,bool A)
{
if (idx == N)return time;
int&ret = cache[idx][time][A];
if (ret != -1)return ret;
ret = INF;
if (A)
{
//A machine
ret = min(ret, f(idx + 1, time + v[idx].first, true));
//B machine
if (time > v[idx].second) ret = min(ret, f(idx + 1, time - v[idx].second, true) + v[idx].second);
else ret = min(ret, f(idx + 1, v[idx].second - time, false) + time);
}
else
{
//A machine
if (time > v[idx].first)ret = min(ret, f(idx + 1, time - v[idx].first, false) + v[idx].first);
else ret = min(ret, f(idx + 1, v[idx].first-time, true) + time);
//B machine
ret = min(ret, f(idx + 1, time + v[idx].second, false));
}
return ret;
}
int main()
{
memset(cache, -1, sizeof(cache));
cin >> N;
for (int i = 0; i<N; i++)
{
int a, b;
cin >> a >> b;
v.push_back({a, b});
}
cout << f(0, 0, 0);
}
풀고 나서 다른 채점자들을 확인해보니 저의 풀이가 시간,공간복잡도가 비효율적인 것 같았습니다.
다른 분의 코드를 확인해보니 바텀업으로 구현하신 걸로 보아 코드를 고치긴 해야할 것 같네요.
#17528 #boj #백준 #two machines #DP
'📌BOJ 알고리즘 트레이닝' 카테고리의 다른 글
| [BOJ][백준]lazy propagation-17611 직각다각형 (0) | 2019.10.15 |
|---|---|
| [BOJ][백준]브루트 포스-17610번 양팔저울 (0) | 2019.10.13 |
| [BOJ][백준]Simulation-17135번 캐슬 디팬스 (0) | 2019.04.11 |
| BFS-1600번 말이 되고픈 원숭이 (0) | 2019.04.04 |
| DP-3114번 사과와 바나나 (0) | 2019.04.04 |
https://www.acmicpc.net/problem/17528
17528번: Two Machines
문제 스케줄링 최적화 회사인 SOPT 에 완료해야 할 n개의 작업 t1, t2, ..., tn 이 있다. SOPT 회사는 두 대의 머신 A 와 B 를 보유하고 있다. 각 작업 ti를 완료하기 위해 SOPT 는 머신 A 와 B 둘 중에 오직 하나를 선택할 수 있다. 작업 ti를 완료하기 위해 머신 A를 선택하면 ai시간이 걸리고 머신 B를 선택하면 bi 시간이 걸린다. 각 머신은 어느 순간에 최대 하나의 작업만 수행할 수 있으며, 한 작업이 시작되면 그 작
www.acmicpc.net
문제
스케줄링 최적화 회사인 SOPT 에 완료해야 할 n개의 작업 t1, t2, ..., tn 이 있다. SOPT 회사는 두 대의 머신 A 와 B 를 보유하고 있다. 각 작업 ti를 완료하기 위해 SOPT 는 머신 A 와 B 둘 중에 오직 하나를 선택할 수 있다. 작업 ti를 완료하기 위해 머신 A를 선택하면 ai시간이 걸리고 머신 B를 선택하면 bi 시간이 걸린다. 각 머신은 어느 순간에 최대 하나의 작업만 수행할 수 있으며, 한 작업이 시작되면 그 작업을 완료하기 전까지 다른 작업을 그 머신에서 수행할 수 없다. SOPT 는 모든 작업을 완료하기 위한 최소의 완료 시간을 구하고자 한다.
예를 들어, 세 개의 작업이 t1, t2, t3가 주어져 있고 a1 = 2, b1 = 3, a2 = 5, b2 = 3, a3 = 2, b3 = 7라고 하자. 완료 시간을 최소화하기 위해서는 작업 t1, t3는 머신 A에, 작업 t2는 머신 B에 할당한다. 머신 A는 작업 t1, t3를 완료하는데 2 + 2 = 4 시간이 걸리고 머신 B는 작업 t2를 완료하는데 3 시간이 걸린다. 따라서 최소 완료 시간은 4 시간이 된다. n개의 작업 t1, t2, ..., tn 과 각 머신에서 각 작업들을 수행하는 데 걸리는 시간들이 주어질 때, 모든 작업들을 완료하기 위해 걸리는 시간의 최솟값을 구하는 프로그램을 작성하시오.
입력
입력은 표준입력을 사용한다. 첫 번째 줄에 작업의 개수를 나타내는 양의 정수 n (1 ≤ n ≤ 250)이 주어진다. 다음 n개의 줄에서 i번째 줄에는 두 개의 정수 ai, bi (1 ≤ ai, bi ≤ 250)가 주어진다. 여기서 ai와 bi는 각각 작업 ti를 머신 A와 B에서 완료하는데 걸리는 시간이다.
출력
출력은 표준출력을 사용한다. 모든 작업 t1, t2, ..., tn을 완료하기 위한 최소의 완료시간을 한 줄에 출력한다.
****************************************************************************************************
참 이상한 문제였습니다. 분명 풀어본 것 같았고, 흔히 말하는 웰노운 문제 같았고, 시간 과 크기 제한도 크지 않은 것 같았습니다. 하지만 몇시간동안 고민한 문제인 two machine문제를 리뷰해보자면,
처음에 직관적으로 생각한 풀이는N^5의 [idx][A머신의 시간할당량][B머신의 시간할당량]풀이였으나 250^5=???
어림도없는 접근이었습니다. 아,근데 이렇게 간단해보이는 문제인데 푼사람은 적고, 정답률은 높으니 (새로운 문제풀때는 solved.ac꺼두고 하는 편입니다.) 풀이가 딴곳으로 샜다는 느낌을 받고 그리디로 접근을 해보았습니다.
생각한 그리디 접근은 2가지였는데,
1)a작업시간 순 정렬,b작업시간 순 정렬 후 최적의 해 구하기
2)|a작업시간-b작업시간|순 정렬 후 최적의 해 구하기
하지만 두가지 전부 이 반례가 존재합니다.
5
10 5
9 4
8 3
7 2
6 1
//answer:10
다시 돌고돌아 dp풀이를 생각했는데, A와B머신의 작업량을 모두 따로 저장해야할 필요가 있을까? 부터 접근을 하여,
[idx][한 머신의 남은 작업량][A머신 or B머신]으로 배열잡기에 성공했습니다.

예시로 설명을 해보자면, 먼저 A머신에 13만큼의 작업량이 쌓아져 있다면,
1의경우, A머신에 7만큼의 작업량이 추가되면 그냥 바로 작업량을 추가해 주면됩니다.
2의경우, A머신에 있는 작업량을 초과하는 B의 작업을 수행하려면 A머신에 누적된 작업량을 수행 한 후에,
B머신에 남은 작업량을 할당해줍니다.
3의경우, A머신에 할당된 작업량보다 B의 작업량이 적으므로 B의 작업량만큼 작업을 수행하면 됩니다.
여기서 작업을 수행한다는 말은 시간이 소요된다는 의미로 해석하면 되겠습니다.
수행되는 과정이 lazy propagation이랑 느낌이 비슷하네요.
#include <iostream>
#include <vector>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_N = 250 + 2, INF = 987654321;
int N, cache[MAX_N][MAX_N*MAX_N][2];
vector<pair<int, int>>v;
int f(int idx, int time,bool A)
{
if (idx == N)return time;
int&ret = cache[idx][time][A];
if (ret != -1)return ret;
ret = INF;
if (A)
{
//A machine
ret = min(ret, f(idx + 1, time + v[idx].first, true));
//B machine
if (time > v[idx].second) ret = min(ret, f(idx + 1, time - v[idx].second, true) + v[idx].second);
else ret = min(ret, f(idx + 1, v[idx].second - time, false) + time);
}
else
{
//A machine
if (time > v[idx].first)ret = min(ret, f(idx + 1, time - v[idx].first, false) + v[idx].first);
else ret = min(ret, f(idx + 1, v[idx].first-time, true) + time);
//B machine
ret = min(ret, f(idx + 1, time + v[idx].second, false));
}
return ret;
}
int main()
{
memset(cache, -1, sizeof(cache));
cin >> N;
for (int i = 0; i<N; i++)
{
int a, b;
cin >> a >> b;
v.push_back({a, b});
}
cout << f(0, 0, 0);
}
풀고 나서 다른 채점자들을 확인해보니 저의 풀이가 시간,공간복잡도가 비효율적인 것 같았습니다.
다른 분의 코드를 확인해보니 바텀업으로 구현하신 걸로 보아 코드를 고치긴 해야할 것 같네요.
#17528 #boj #백준 #two machines #DP
'📌BOJ 알고리즘 트레이닝' 카테고리의 다른 글
| [BOJ][백준]lazy propagation-17611 직각다각형 (0) | 2019.10.15 |
|---|---|
| [BOJ][백준]브루트 포스-17610번 양팔저울 (0) | 2019.10.13 |
| [BOJ][백준]Simulation-17135번 캐슬 디팬스 (0) | 2019.04.11 |
| BFS-1600번 말이 되고픈 원숭이 (0) | 2019.04.04 |
| DP-3114번 사과와 바나나 (0) | 2019.04.04 |