
저희 학교 알고리즘 과목에 첫 번째 과제로 피보나치킨이 등장했습니다. 입력 제한이 3억일 때, 피보나치 배열을 어느 제한까지 구해야 하는지, 배열 인덱싱과 stringToint의 형 변환 등 다양한 요소가 포함되어 있습니다. 단순 구현으로 풀이해도 되지만, 다양한 풀이법이 존재하고 피보나치수열과 제켄도르프 정리는 상당히 흥미로운 내용이기 때문에 소개해 드리려고 합니다. 코드는 모두 올리진 않겠습니다. 학교 과제 내용이기도 해서..
1. DP를 이용한 풀이 방법
가장 일반적인 방법입니다. f(n)=f(n-1)+f(n-2) 라는 간단한 점화식을 활용해 피보나치 수를 구한 다음, n보다 작지만 가장 큰 피보나치 수를 빼며 그 인덱스를 치킨 합에 더해주고 n에 피보나치 수를 빼고 n을 0으로 만들면 종료합니다. 피보나치 수를 반복문이나 재귀로 구하면 그게 곧 DP입니다. 단, 재귀로 구할 경우 메모이제이션을 하지 않으면 DP풀이가 아니므로 시간 복잡도가 급격히 올라갑니다.
while(n){
int fib,chicken;
for(int i=1;i<MAX_N;i++){
if(fibo[i]<=n){
fib=fibo[i];
chicken=fibo[i-1];
}
else break;
}
n-=fib;
ans+=chicken;
}피보나치 수를 구하는 과정을 끝낸 후, 입력인 n을 0으로 만드는 과정 중 출력할 수 ans에 chicken을 더한 후 최종적으로 ans를 출력하면 됩니다. 43번째 피보나치 수가 4억을 넘기 때문에 MAX_N을 44로 두고 풀면 됩니다. 시간복잡도를 구하는 건 조금 까다롭습니다. MAX_N, 즉 피보나치수열의 길이의 최댓값을 M으로 두고, 제켄도르프로 표현되는 항의 개수의 최댓값을 K로 둘 때, O(KM)입니다. 입력 N이 3억 일 때 M은 45, K는 M의 절반보다 낮음이 보장되므로 시간 복잡도는 매우 낮습니다.
단, 재귀함수를 다음과 같이 메모이제이션을 생략했을 경우 시간 복잡도는 O(2^N)이기 때문에 시간 복잡도가 매우 커집니다.
int fibo(int n){
if(now<=1)return n;
return fibo(n-1)+fibo(n-2);
}
2. DP와 이분탐색을 이용한 풀이 방법
앞서 반복문으로 구했던 다음 과정을 이분 탐색으로 구할 수 있습니다.
N보다 작거나 같으면서 가장 큰 피보나치 수열의 수와 그 인덱스
피보나치수열의 길이의 최댓값을 M으로 두고, 제켄도르프로 표현되는 항의 개수의 최댓값을 K로 둘 때, O(log(K) M)입니다. K가 아주 작으므로 굳이 이분 탐색을 쓸 필요는 없지만 풀이과정이 이분 탐색과 꼭 맞는 조건입니다.
3. Hofstadter의 G-Sequence
놀랍게도 이 문제는 피보나치의 수열을 구하지 않고도 풀 수 있습니다. 정답으로 표현되는 수열을 다음과 같이 재귀적으로 연결 해 봅시다.

이처럼 체크표시로 재귀적으로 연결 하고, 밑에서 위로, 왼쪽에서 오른쪽으로 수를 채워져 나가면
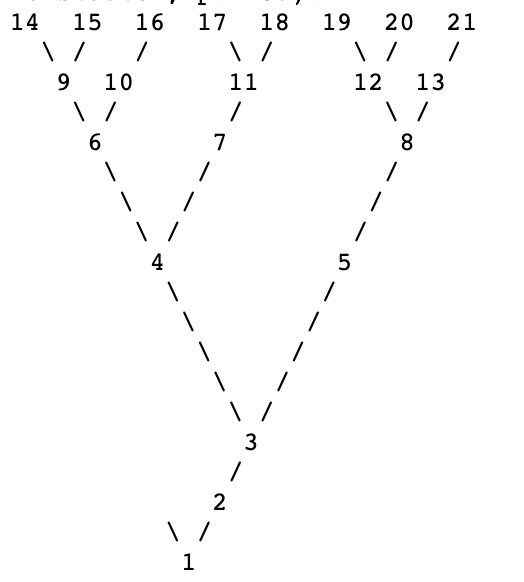
다음과 같이 수열의 정답을 바로 알 수 있습니다. 원소 바로 밑의 수가 답이 되는데, 예를 들어 입력 11의 답은 7(G(11)=7) , 19의 답은 12가 되죠.(G(19)=12)
이와 같은 재귀적인 수열을 점화식으로 나타낼 수 있음이 증명되었습니다. (단, G(0)은 0)
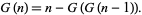
이 되고, 결과적으로는 피보나치수열 없이 답을 구할 수 있습니다. 하지만 여기서 아래 식을 도출해 낼 수 있습니다.
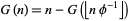
[]는 floor 연산이고, 기호는 golden ratio, 즉 황금비입니다. 그 유명한 피보나치 수와 황금 비의 관계를 여기서도 확인할 수 있습니다.
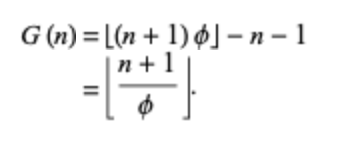
최종적으로 식을 다음과 같이 정리하면, floor((n+1)/golden_ratio)로 간단히 답을 구할 수 있게 되죠. 황금비를 미리 계산해두고 long double형으로 저장해두면, 시간 복잡도 O(1), 상수 시간에 답을 구할 수 있습니다.
cout<<(long long)floor((long double)(n+1)/golden_ratio); //답 출력n입력이 얼마가 들어오든 계산할 수 있게됩니다. 단, long long과 long double이 연산 가능한 범위까지 만 이요. 이론상으로는 10^1000 입력이 들어와도 연산이 가능하지만 C++로는 큰 수 처리가 매우 까다로우니 python을 사용하면 조금 느리겠지만 연산이 가능해집니다.
부록: 제켄도르프 정리의 응용
문제 설명에 사용된 제켄도르프 정리는 이곳저곳에서 응용되는데, 특히 게임이론의 스프라그-그런디 정리에서 그런디 수의 규칙성을 찾을 때 사용됩니다.
https://newdeal123.tistory.com/52
[BOJ][백준] 2373번: Fibonacci Game
https://www.acmicpc.net/problem/2373 2373번: Fibonacci Game 당신은 N(2≤N≤1,000,000)개의 구슬을 가지고 다음과 같은 게임을 하려고 한다. 게임은 두 사람이 번갈아 가면서 진행하며, 1번 사람이 몇 개의 구..
newdeal123.tistory.com
문제 설명을 읽어보시면 구슬 더미에서 내가 1개 가져오고, 다음 사람은 2개 이하로 가져가고, 내가 4개 이하로 가져오는 구슬 가져오기 게임에서 어떻게 전혀 연관성이 없어 보이는 제켄도르프 표현이 튀어나오고, 피보나치 수가 중요하게 쓰이는지는 흥미로운 주제입니다.
출처:
Gault, D. and Clint, M. "'Curiouser and Curiouser,' Said Alice. Further Reflections on an Interesting Recursive Function." Internat. J. Computer Math. 26, 35-43, 1988.
Gould, H. W.; Kim, J. B.; and Hoggatt, V. E. Jr. "Sequences Associated with T-Ary Coding of Fibonacci's Rabbits." Fib. Quart. 15, 311-318, 1977.
Granville, V. and Rasson, J. P. "A Strange Recursive Relation." J. Number Th. 30, 238-241, 1988.
Grytczuk, J. "Another Variation on Conway's Recursive Sequence." Discr. Math. 282, 149-161, 2004.
Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 137, 1989.
Sloane, N. J. A. Sequence A005206/M0436 in "The On-Line Encyclopedia of Integer Sequences."
'📑코드 포스트잇' 카테고리의 다른 글
| 라빈-카프 알고리즘 기본형(Rabin-Karp Algorithm) (1) | 2020.09.21 |
|---|---|
| 유전 알고리즘 (0) | 2020.08.13 |
| c++ 기하 문제들 풀기위한 vector2 구조체 (0) | 2020.03.30 |
| C++ 두 선분의 교차 여부 (0) | 2020.03.24 |
| 네트워크 플로우(일반적 구현, 구조체로 구현) (0) | 2020.02.19 |

저희 학교 알고리즘 과목에 첫 번째 과제로 피보나치킨이 등장했습니다. 입력 제한이 3억일 때, 피보나치 배열을 어느 제한까지 구해야 하는지, 배열 인덱싱과 stringToint의 형 변환 등 다양한 요소가 포함되어 있습니다. 단순 구현으로 풀이해도 되지만, 다양한 풀이법이 존재하고 피보나치수열과 제켄도르프 정리는 상당히 흥미로운 내용이기 때문에 소개해 드리려고 합니다. 코드는 모두 올리진 않겠습니다. 학교 과제 내용이기도 해서..
1. DP를 이용한 풀이 방법
가장 일반적인 방법입니다. f(n)=f(n-1)+f(n-2) 라는 간단한 점화식을 활용해 피보나치 수를 구한 다음, n보다 작지만 가장 큰 피보나치 수를 빼며 그 인덱스를 치킨 합에 더해주고 n에 피보나치 수를 빼고 n을 0으로 만들면 종료합니다. 피보나치 수를 반복문이나 재귀로 구하면 그게 곧 DP입니다. 단, 재귀로 구할 경우 메모이제이션을 하지 않으면 DP풀이가 아니므로 시간 복잡도가 급격히 올라갑니다.
while(n){
int fib,chicken;
for(int i=1;i<MAX_N;i++){
if(fibo[i]<=n){
fib=fibo[i];
chicken=fibo[i-1];
}
else break;
}
n-=fib;
ans+=chicken;
}피보나치 수를 구하는 과정을 끝낸 후, 입력인 n을 0으로 만드는 과정 중 출력할 수 ans에 chicken을 더한 후 최종적으로 ans를 출력하면 됩니다. 43번째 피보나치 수가 4억을 넘기 때문에 MAX_N을 44로 두고 풀면 됩니다. 시간복잡도를 구하는 건 조금 까다롭습니다. MAX_N, 즉 피보나치수열의 길이의 최댓값을 M으로 두고, 제켄도르프로 표현되는 항의 개수의 최댓값을 K로 둘 때, O(KM)입니다. 입력 N이 3억 일 때 M은 45, K는 M의 절반보다 낮음이 보장되므로 시간 복잡도는 매우 낮습니다.
단, 재귀함수를 다음과 같이 메모이제이션을 생략했을 경우 시간 복잡도는 O(2^N)이기 때문에 시간 복잡도가 매우 커집니다.
int fibo(int n){
if(now<=1)return n;
return fibo(n-1)+fibo(n-2);
}
2. DP와 이분탐색을 이용한 풀이 방법
앞서 반복문으로 구했던 다음 과정을 이분 탐색으로 구할 수 있습니다.
N보다 작거나 같으면서 가장 큰 피보나치 수열의 수와 그 인덱스
피보나치수열의 길이의 최댓값을 M으로 두고, 제켄도르프로 표현되는 항의 개수의 최댓값을 K로 둘 때, O(log(K) M)입니다. K가 아주 작으므로 굳이 이분 탐색을 쓸 필요는 없지만 풀이과정이 이분 탐색과 꼭 맞는 조건입니다.
3. Hofstadter의 G-Sequence
놀랍게도 이 문제는 피보나치의 수열을 구하지 않고도 풀 수 있습니다. 정답으로 표현되는 수열을 다음과 같이 재귀적으로 연결 해 봅시다.

이처럼 체크표시로 재귀적으로 연결 하고, 밑에서 위로, 왼쪽에서 오른쪽으로 수를 채워져 나가면

다음과 같이 수열의 정답을 바로 알 수 있습니다. 원소 바로 밑의 수가 답이 되는데, 예를 들어 입력 11의 답은 7(G(11)=7) , 19의 답은 12가 되죠.(G(19)=12)
이와 같은 재귀적인 수열을 점화식으로 나타낼 수 있음이 증명되었습니다. (단, G(0)은 0)
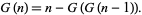
이 되고, 결과적으로는 피보나치수열 없이 답을 구할 수 있습니다. 하지만 여기서 아래 식을 도출해 낼 수 있습니다.
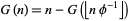
[]는 floor 연산이고, 기호는 golden ratio, 즉 황금비입니다. 그 유명한 피보나치 수와 황금 비의 관계를 여기서도 확인할 수 있습니다.
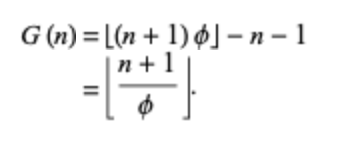
최종적으로 식을 다음과 같이 정리하면, floor((n+1)/golden_ratio)로 간단히 답을 구할 수 있게 되죠. 황금비를 미리 계산해두고 long double형으로 저장해두면, 시간 복잡도 O(1), 상수 시간에 답을 구할 수 있습니다.
cout<<(long long)floor((long double)(n+1)/golden_ratio); //답 출력n입력이 얼마가 들어오든 계산할 수 있게됩니다. 단, long long과 long double이 연산 가능한 범위까지 만 이요. 이론상으로는 10^1000 입력이 들어와도 연산이 가능하지만 C++로는 큰 수 처리가 매우 까다로우니 python을 사용하면 조금 느리겠지만 연산이 가능해집니다.
부록: 제켄도르프 정리의 응용
문제 설명에 사용된 제켄도르프 정리는 이곳저곳에서 응용되는데, 특히 게임이론의 스프라그-그런디 정리에서 그런디 수의 규칙성을 찾을 때 사용됩니다.
https://newdeal123.tistory.com/52
[BOJ][백준] 2373번: Fibonacci Game
https://www.acmicpc.net/problem/2373 2373번: Fibonacci Game 당신은 N(2≤N≤1,000,000)개의 구슬을 가지고 다음과 같은 게임을 하려고 한다. 게임은 두 사람이 번갈아 가면서 진행하며, 1번 사람이 몇 개의 구..
newdeal123.tistory.com
문제 설명을 읽어보시면 구슬 더미에서 내가 1개 가져오고, 다음 사람은 2개 이하로 가져가고, 내가 4개 이하로 가져오는 구슬 가져오기 게임에서 어떻게 전혀 연관성이 없어 보이는 제켄도르프 표현이 튀어나오고, 피보나치 수가 중요하게 쓰이는지는 흥미로운 주제입니다.
출처:
Gault, D. and Clint, M. "'Curiouser and Curiouser,' Said Alice. Further Reflections on an Interesting Recursive Function." Internat. J. Computer Math. 26, 35-43, 1988.
Gould, H. W.; Kim, J. B.; and Hoggatt, V. E. Jr. "Sequences Associated with T-Ary Coding of Fibonacci's Rabbits." Fib. Quart. 15, 311-318, 1977.
Granville, V. and Rasson, J. P. "A Strange Recursive Relation." J. Number Th. 30, 238-241, 1988.
Grytczuk, J. "Another Variation on Conway's Recursive Sequence." Discr. Math. 282, 149-161, 2004.
Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid. New York: Vintage Books, p. 137, 1989.
Sloane, N. J. A. Sequence A005206/M0436 in "The On-Line Encyclopedia of Integer Sequences."
'📑코드 포스트잇' 카테고리의 다른 글
| 라빈-카프 알고리즘 기본형(Rabin-Karp Algorithm) (1) | 2020.09.21 |
|---|---|
| 유전 알고리즘 (0) | 2020.08.13 |
| c++ 기하 문제들 풀기위한 vector2 구조체 (0) | 2020.03.30 |
| C++ 두 선분의 교차 여부 (0) | 2020.03.24 |
| 네트워크 플로우(일반적 구현, 구조체로 구현) (0) | 2020.02.19 |
