문제를 풀다보면 때때로 기댓값을 묻는 문제들이 있습니다. 제목은 기댓값 알고리즘이지만 사실 거창한 알고리즘은 없고,
기댓값 문제의 접근방식과 대략적인 용어설명을 하려고 합니다. 사실 처음들었을때 기댓값이라는건 약간 생소할 수 있습니다.
하지만 대다수의 확률을묻는 문제들이 dp로해결하는것 과 같이, 기댓값문제들도 거진dp로 해결할 수 있습니다.
제일 쉬운 예제를 한번 보면,
https://www.acmicpc.net/problem/13250
13250번: 주사위 게임
효빈이는 1부터 6까지 수가 적혀있는 6면 주사위를 가지고 있다. 매번 주사위를 던질 때마다 주사위의 윗 면에 적힌 수 만큼 사탕을 받게 된다. 효빈이가 적어도 N개의 사탕을 받기 위해 주사위를 던져야 하는 횟수의 기댓값을 구하는 프로그램을 작성하시오.
www.acmicpc.net
문제
효빈이는 1부터 6까지 수가 적혀있는 6면 주사위를 가지고 있다. 매번 주사위를 던질 때마다 주사위의 윗 면에 적힌 수 만큼 사탕을 받게 된다. 효빈이가 적어도 N개의 사탕을 받기 위해 주사위를 던져야 하는 횟수의 기댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N ≤ 1,000,000)
출력
첫째 줄에 사탕을 적어도 N개 받기 위해 주사위를 던져야 하는 횟수의 기댓값을 출력한다. 정답과의 절대/상대 오차는 10-9까지 허용한다.
기댓값의 사전적 정의는 다음과 같습니다.
"각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값이다. 이것은 어떤 확률적 사건에 대한 평균의 의미로 생각할 수 있다."
조금은 의미가 딱딱하게 다가오는데, 예제의 기댓값을 해석해보면: 효빈이가 적어도 N개의 사탕을 받기위헤서는 평균적으로 주사위를 X번을 던저야한다. 라고 해석할수 있습니다. 7개의 사탕을 받기위해서는 평균적으로 2.52번의 주사위를 던져야한다는 것입니다.
그렇다면 점화식을 어떻게 접근해야 할까요? 아까 사전적 정의를 보다시피
기댓값 = 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값 입니다.
이를 예제에 대입해보면, 각 사건이 벌어졌을때의 이득은 주사위를 던지는 횟수입니다. 그 사건이 벌어질 확률은
모든 행위가 1/6으로 동일함을 알 수 있습니다.(주사위6면 중 1개). 확률은 대게 글로만보면 어렵기마련입니다.
정답코드를 봅시다.
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_N = 1000000 + 2;
int N;
double cache[MAX_N];
double f(int n)
{
if (n <= 0) return 0.0;
double &ret = cache[n];
if (ret > -0.5) return ret;
ret = 0.0;
for (int i = 1; i <= 6; i++)
ret += (f(n - i) + 1)/6.0;
return ret;
}
int main()
{
memset(cache, -1, sizeof(cache));
cin >> N;
cout << fixed;
cout.precision(11);
cout << f(N);
}함수 f(n)을 n개의 사탕이 남았을때, 던져야하는 주사위횟수의 기댓값이라고 정의를 합시다.
for문을 보면, 주사위의 면이(1~6) 나왔을때의 기댓값을 모두 더하고있습니다.
주사위의 면이 1이나왔을때, 사탕은 n-1개가 남았을것이고, 주사위 던지는횟수가 1회 늘었으므로 f(n-i)+1입니다.
거기에 주사위의 면이 1이나올 확률은 1/6이므로 /6.0을 해주면됩니다. 확률을 구하는것과 dp점화식은 동일하게 짜면되지만,
기댓값에서 다른 점은 각각을 더해줘야한다는 사실입니다.
비슷한 난이도의 다른 예제를 봅시다.
https://www.acmicpc.net/problem/13255
13255번: 동전 뒤집기
첫째 줄에 동전의 개수 N (1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 K (1 ≤ K ≤ 50)이 주어진다. 셋째 줄에는 A[i] (1 ≤ A[i] ≤ N)가 주어진다.
www.acmicpc.net
문제
N개의 동전이 탁자 위에 놓여져 있다. 동전은 모두 앞면이 위를 향하고 있다.
K개의 정수 A[i]가 주어진다. 가장 처음에 A[1]개의 동전을 랜덤하게 골라서 뒤집는다. 그 다음에는 A[2]개의 동전을 랜덤하게 골라서 뒤집는다. 이 과정을 계속해서 반복하고, 마지막에는 A[K]개의 동전을 랜덤하게 골라서 뒤집는다.
모든 과정을 완료했을 때, 앞면이 위를 향하는 동전 개수의 기댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 동전의 개수 N (1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 K (1 ≤ K ≤ 50)이 주어진다. 셋째 줄에는 A[i] (1 ≤ A[i] ≤ N)가 주어진다.
출력
모든 과정을 완료한 후에 앞면이 위를 향하는 동전 개수의 기댓값을 출력한다.
정답과의 절대/상대 오차는 10-9까지 허용한다.
이 문제하단의 힌트에서 문제의 접근방식을 친절히 알려주고 있습니다.
예제 1
3
2
2 2
예제 1의 경우에 첫 단계에서 동전 2개를 뒤집어야 한다. 두 번째 단계에는 다음과 같은 두 가지 상황이 가능하다.
- 뒷면 2개를 골라서 뒤집는다. (확률: 1/3) 앞면의 개수는 3개가 된다.
- 앞면 1개와 뒷면 1개를 골라서 뒤집는다. (확률: 2/3) 앞면의 개수는 1개가 된다.
기댓값은 1/3*3 + 2/3*1 = 5/3 이다.
함수를 f(남은 앞면이 위를향하는 동전의 수, A배열의 idx)라 두고, idx를 하나씩 늘려가면서 A배열의 값만큼 동전을 뒤집으면 됩니다. 문제의 예제3번을 예로들자면,
예제 3
10
6
2 7 1 8 2 8
(U:동전의 앞면이 위를 향함,D:동전의 뒷면이 위를 향함)
처음상태는 UUUUU UUUUU 입니다. 여기서 첫째로 2개의 동전을 뒤집어야 하므로,
우리가 고려해야할 상태는 1개밖에 없습니다.
DDUUU UUUUU (동전의 순서를 고려하지 않음)
여기서 두번째로 7개의 동전을 뒤집어야하는데, 여기서 세가지의 상태로 나뉘어집니다.
(D뒤집는개수,U뒤집는개수)=(0,7),(1,6),(2,5)
DDDDD DDDDU
DUDDD DDDUU
UUDDD DDUUU
...
이런 방식으로 진행을 하면되는데, 여기서 이전문제와 다른점은 확률이 각 상태마다 다르다는점입니다.
이전 문제에서는 주사위의 상태가 동일하니 모두1/6이 나왔지만 이문제에서는 동전의 상태가 다 다르기때문에
우리가 확률을 계산해 주어야합니다. 다행히 우리는 comb함수로 이를 해결할 수 있습니다.
#include <iostream>
#include <string.h>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX_N=1000+2;
int N,K;
vector<int>order;
double cache[MAX_N][50+2],cache2[MAX_N][MAX_N];
double comb(int n,int r)
{
if(r==0||n==r)return 1.0;
double&ret=cache2[n][r];
if(ret>-0.5)return ret;
return ret=comb(n-1,r-1)+comb(n-1,r);
}
double f(int upCoin,int idx)
{
if(idx==K)return upCoin;
double&ret=cache[upCoin][idx];
if(ret>-0.5)return ret;
ret=0.0;
int downCoin=N-upCoin;
//i:upCoin selected, j:downCoint selected
for(int i=0;i<=order[idx];i++)
{
int j=order[idx]-i;
if(downCoin<j||upCoin<i)continue;
ret+=f(upCoin-i+j,idx+1)*(comb(upCoin,i)*comb(downCoin,j))/comb(N,order[idx]);
}
return ret;
}
int main()
{
cin>>N>>K;
memset(cache,-1,sizeof(cache));
memset(cache2,-1,sizeof(cache2));
order.resize(K);
for(auto&i:order)cin>>i;
cout<<fixed;
cout.precision(9);
cout<<f(N,0);
}
확률 계산이 (comb(upCoin,i)*comb(downCoin,j))/comb(N,order[idx]) 로 까다로운 점을 제외하면
이전문제와 크게 다르지 않습니다.
하지만 모든문제에서 dp를 쓸수있는건 아닙니다.
https://www.acmicpc.net/problem/13347
13347번: Lost In The Woods
The first line contains two integers N and M, where N is the number of clearings in the woods (2 ≤ N ≤ 20), and M is the total number of paths between clearings. The clearings are numbered 0 through N − 1, such that clearing 0 is the one where your friend
www.acmicpc.net
다음문제와 같이 양방향그래프가 주어져있을때, 출발노드는0번노드이고, 도착노드는 N-1입니다.
노드 이동시간이 1일때, 도착노드에 도착하는 기댓값을 구하는문제입니다. 간단해보이는데, 이전과같은 접근법을
시도하면 루프의 늪에 빠지게 됩니다. 그리고 우리가 사용하던 재귀dp는 무한루프가 생겼을때, 대처를 못합니다.
함수인자에 depth를 추가해 몇만번 이상 depth가 누적되면 종료하는 방식도있지만, depth의 종료조건을 계산하기 까다롭고, depth의 길이만큼 메모이제이션의 크기도 엄청나게 불어날것이며 그에따라 메모리초과를 일으키거나 매우 비효율적으로 알고리즘이 동작할것입니다.
이를 해결하기위해, '확률의 이동'을 새로 생각해 봅시다.
예제 1
3 3
0 1
1 2
0 2
다음 그래프에서 (node번호,확률) 이라고했을때
초기그래프는 다음과 같이 둘 수 있습니다. 0번노드에 1.0확률이 있습니다.

여기서 1.0은 1/2확률로 1번노드로 이동을하고, 1/2확률로 2번노드로 이동을 합니다.
이동할때 해당확률에 1/2를 곱해줍시다.

2초일때의 상황입니다. 1번노드에 0.5확률이있고, 2번노드에 0.5확률이 있게되는데, 여기서 2번노드는 도착노드이므로
도착확률에 현재 시간을 곱해줍시다. (sum+=0.5*2) 그리고 1번노드의 0.5도 1/2확률로 0번노드로 이동을하고, 1/2확률로 2번노드로 이동을합니다.
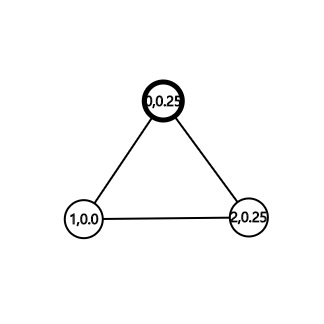
3초일때의 상황입니다. 마찬가지로 2번노드에 0.25가 도착했으므로 (sum+=0.25*3)을 하면됩니다. 0번노드의 0.25는 또 1/2확률로 1,2번노드로 이동을하고....
를 반복해주면됩니다. 그리고 이를 구현해주면 됩니다.
#include <iostream>
#include <algorithm>
#include <string.h>
#include <vector>
using namespace std;
int n, m;
vector<int> adj[21];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<double> node(n, 0.0);
node[0] = 1.0;
double ret = 0.0;
// Each step:
for (int i = 1; i < 10000; i++)
{
vector<double> new_node(n, 0.0);
for (int u = 0; u < n; u++)
for (int v : adj[u])
new_node[v] += node[u] / adj[u].size();
ret += i * new_node[n - 1];
node = new_node;
node[n - 1] = 0.0;
}
cout << fixed;
cout.precision(8);
cout << ret;
}
1만번정도만 반복문을 돌면됩니다. 몇번정도 반복문을 돌아야하는지는 공식이있을텐데 아직 찾지는 못했습니다.
양방향그래프이므로 입력받을때 간선을 양방향으로 추가하는것도 잊지맙시다.
추천문제
복권 + 은행: https://www.acmicpc.net/problem/13258
13258번: 복권 + 은행
두 번째 예제의 경우에 첫 주가 지난 후 1/3의 확률로 (3, 2, 2)가, 1/3의 확률로 (2, 3, 2)가, 1/3의 확률로 (2, 2, 3)이 된다. 둘째 주에 (3, 2, 2)는 기댓값이 3.4286이 되고, (2, 3, 2)와 (2, 2, 3)은 기댓값이 2.2857이 된다. 따라서, 기댓값은 2.66667이다.
www.acmicpc.net
토끼의 이동: https://www.acmicpc.net/problem/13247
13247번: 토끼의 이동
첫째 줄에 게임판의 색상이 주어진다. 게임판의 크기(N)는 2보다 크거나 같고, 17보다 작거나 같으며, W는 흰색, B는 검정색, R은 빨간색을 나타낸다. 둘째 줄에는 토끼의 수 r (1 ≤ r ≤ N)이 주어진다.
www.acmicpc.net
랜덤 소트:https://www.acmicpc.net/problem/1521
1521번: 랜덤 소트
첫째 줄에 순열의 크기 N이 주어진다. 둘째 줄에 순열에 들어있는 수 N개가 주어진다. 이 수는 모두 1보다 크거나 같고, N보나 작거나 같으며, 같은 수는 2번 이상 주어지지 않는다. 또, N은 8보다 작거나 같은 자연수이다.
www.acmicpc.net
Following Flow:https://www.acmicpc.net/problem/10894
10894번: Following Flow
세상은 N+1개의 정점으로 이루어져 있는데, 각 정점은 0에서 N까지의 번호가 붙어있다. 각 정점에서는 다른 정점으로 가는 간선이 있는데, 각 간선은 일방통행이며, 각 간선마다 간선을 지나가는데 걸리는 시간이 다르다. 동현이는 세상을 떠돌고 있는데, 0번 지점은 동현이가 현재 있는 위치이고, N번은 동현이의 집이다. 동현이는 집에 도착하기 전까지는 마음이 가는 대로 세상을 떠돌고 싶어한다. 마음이 가는 대로라는 것은 현재 정점에서 다른 정점으로 갈 수 있
www.acmicpc.net
Research Productivity Index:https://www.acmicpc.net/problem/17591
17591번: Research Productivity Index
The first line of the input has a single integer n (1 ≤ n ≤ 100), the number of Angela’s candidate papers. The next line has n space-separated integers giving the probability of each paper getting accepted. Each probability value is given as an integer per
www.acmicpc.net
랜덤 걷기:https://www.acmicpc.net/problem/3946
3946번: 랜덤 걷기
문제 걷기 전에 동전을 던진 다음, 앞 면이면 왼쪽으로 한 칸, 뒷 면이면 오른쪽으로 한 칸 이동하는 방법을 랜덤 걷기라고 한다. 이 랜덤 걷기의 위치의 기댓값은 항상 0이 된다. 즉, 랜덤 걷기를 아무리 많이 한다고 해도, 평균 위치는 처음 시작한 지점과 같다. 랜덤 걷기에서 왼쪽으로 갈 확률과 오른쪽으로 갈 확률, 그리고 동전을 던지는 횟수가 주어졌을 때, 가장 오른쪽 위치의 기댓값을 구하는 프로그램을 작성하시오. 입력 첫째 줄에는 테스트 케이스의 P
www.acmicpc.net
'👨💻코드 포스터' 카테고리의 다른 글
| 코테 준비 알고리즘 - 정렬 (0) | 2021.04.27 |
|---|---|
| 게임 이론(스프라그-그런디 이론) (0) | 2020.04.27 |
| Heavy-Light Decomposition 알고리즘 (0) | 2020.01.28 |
문제를 풀다보면 때때로 기댓값을 묻는 문제들이 있습니다. 제목은 기댓값 알고리즘이지만 사실 거창한 알고리즘은 없고,
기댓값 문제의 접근방식과 대략적인 용어설명을 하려고 합니다. 사실 처음들었을때 기댓값이라는건 약간 생소할 수 있습니다.
하지만 대다수의 확률을묻는 문제들이 dp로해결하는것 과 같이, 기댓값문제들도 거진dp로 해결할 수 있습니다.
제일 쉬운 예제를 한번 보면,
https://www.acmicpc.net/problem/13250
13250번: 주사위 게임
효빈이는 1부터 6까지 수가 적혀있는 6면 주사위를 가지고 있다. 매번 주사위를 던질 때마다 주사위의 윗 면에 적힌 수 만큼 사탕을 받게 된다. 효빈이가 적어도 N개의 사탕을 받기 위해 주사위를 던져야 하는 횟수의 기댓값을 구하는 프로그램을 작성하시오.
www.acmicpc.net
문제
효빈이는 1부터 6까지 수가 적혀있는 6면 주사위를 가지고 있다. 매번 주사위를 던질 때마다 주사위의 윗 면에 적힌 수 만큼 사탕을 받게 된다. 효빈이가 적어도 N개의 사탕을 받기 위해 주사위를 던져야 하는 횟수의 기댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (1 ≤ N ≤ 1,000,000)
출력
첫째 줄에 사탕을 적어도 N개 받기 위해 주사위를 던져야 하는 횟수의 기댓값을 출력한다. 정답과의 절대/상대 오차는 10-9까지 허용한다.
기댓값의 사전적 정의는 다음과 같습니다.
"각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값이다. 이것은 어떤 확률적 사건에 대한 평균의 의미로 생각할 수 있다."
조금은 의미가 딱딱하게 다가오는데, 예제의 기댓값을 해석해보면: 효빈이가 적어도 N개의 사탕을 받기위헤서는 평균적으로 주사위를 X번을 던저야한다. 라고 해석할수 있습니다. 7개의 사탕을 받기위해서는 평균적으로 2.52번의 주사위를 던져야한다는 것입니다.
그렇다면 점화식을 어떻게 접근해야 할까요? 아까 사전적 정의를 보다시피
기댓값 = 각 사건이 벌어졌을 때의 이득과 그 사건이 벌어질 확률을 곱한 것을 전체 사건에 대해 합한 값 입니다.
이를 예제에 대입해보면, 각 사건이 벌어졌을때의 이득은 주사위를 던지는 횟수입니다. 그 사건이 벌어질 확률은
모든 행위가 1/6으로 동일함을 알 수 있습니다.(주사위6면 중 1개). 확률은 대게 글로만보면 어렵기마련입니다.
정답코드를 봅시다.
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAX_N = 1000000 + 2;
int N;
double cache[MAX_N];
double f(int n)
{
if (n <= 0) return 0.0;
double &ret = cache[n];
if (ret > -0.5) return ret;
ret = 0.0;
for (int i = 1; i <= 6; i++)
ret += (f(n - i) + 1)/6.0;
return ret;
}
int main()
{
memset(cache, -1, sizeof(cache));
cin >> N;
cout << fixed;
cout.precision(11);
cout << f(N);
}함수 f(n)을 n개의 사탕이 남았을때, 던져야하는 주사위횟수의 기댓값이라고 정의를 합시다.
for문을 보면, 주사위의 면이(1~6) 나왔을때의 기댓값을 모두 더하고있습니다.
주사위의 면이 1이나왔을때, 사탕은 n-1개가 남았을것이고, 주사위 던지는횟수가 1회 늘었으므로 f(n-i)+1입니다.
거기에 주사위의 면이 1이나올 확률은 1/6이므로 /6.0을 해주면됩니다. 확률을 구하는것과 dp점화식은 동일하게 짜면되지만,
기댓값에서 다른 점은 각각을 더해줘야한다는 사실입니다.
비슷한 난이도의 다른 예제를 봅시다.
https://www.acmicpc.net/problem/13255
13255번: 동전 뒤집기
첫째 줄에 동전의 개수 N (1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 K (1 ≤ K ≤ 50)이 주어진다. 셋째 줄에는 A[i] (1 ≤ A[i] ≤ N)가 주어진다.
www.acmicpc.net
문제
N개의 동전이 탁자 위에 놓여져 있다. 동전은 모두 앞면이 위를 향하고 있다.
K개의 정수 A[i]가 주어진다. 가장 처음에 A[1]개의 동전을 랜덤하게 골라서 뒤집는다. 그 다음에는 A[2]개의 동전을 랜덤하게 골라서 뒤집는다. 이 과정을 계속해서 반복하고, 마지막에는 A[K]개의 동전을 랜덤하게 골라서 뒤집는다.
모든 과정을 완료했을 때, 앞면이 위를 향하는 동전 개수의 기댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 동전의 개수 N (1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 K (1 ≤ K ≤ 50)이 주어진다. 셋째 줄에는 A[i] (1 ≤ A[i] ≤ N)가 주어진다.
출력
모든 과정을 완료한 후에 앞면이 위를 향하는 동전 개수의 기댓값을 출력한다.
정답과의 절대/상대 오차는 10-9까지 허용한다.
이 문제하단의 힌트에서 문제의 접근방식을 친절히 알려주고 있습니다.
예제 1
3
2
2 2
예제 1의 경우에 첫 단계에서 동전 2개를 뒤집어야 한다. 두 번째 단계에는 다음과 같은 두 가지 상황이 가능하다.
- 뒷면 2개를 골라서 뒤집는다. (확률: 1/3) 앞면의 개수는 3개가 된다.
- 앞면 1개와 뒷면 1개를 골라서 뒤집는다. (확률: 2/3) 앞면의 개수는 1개가 된다.
기댓값은 1/3*3 + 2/3*1 = 5/3 이다.
함수를 f(남은 앞면이 위를향하는 동전의 수, A배열의 idx)라 두고, idx를 하나씩 늘려가면서 A배열의 값만큼 동전을 뒤집으면 됩니다. 문제의 예제3번을 예로들자면,
예제 3
10
6
2 7 1 8 2 8
(U:동전의 앞면이 위를 향함,D:동전의 뒷면이 위를 향함)
처음상태는 UUUUU UUUUU 입니다. 여기서 첫째로 2개의 동전을 뒤집어야 하므로,
우리가 고려해야할 상태는 1개밖에 없습니다.
DDUUU UUUUU (동전의 순서를 고려하지 않음)
여기서 두번째로 7개의 동전을 뒤집어야하는데, 여기서 세가지의 상태로 나뉘어집니다.
(D뒤집는개수,U뒤집는개수)=(0,7),(1,6),(2,5)
DDDDD DDDDU
DUDDD DDDUU
UUDDD DDUUU
...
이런 방식으로 진행을 하면되는데, 여기서 이전문제와 다른점은 확률이 각 상태마다 다르다는점입니다.
이전 문제에서는 주사위의 상태가 동일하니 모두1/6이 나왔지만 이문제에서는 동전의 상태가 다 다르기때문에
우리가 확률을 계산해 주어야합니다. 다행히 우리는 comb함수로 이를 해결할 수 있습니다.
#include <iostream>
#include <string.h>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX_N=1000+2;
int N,K;
vector<int>order;
double cache[MAX_N][50+2],cache2[MAX_N][MAX_N];
double comb(int n,int r)
{
if(r==0||n==r)return 1.0;
double&ret=cache2[n][r];
if(ret>-0.5)return ret;
return ret=comb(n-1,r-1)+comb(n-1,r);
}
double f(int upCoin,int idx)
{
if(idx==K)return upCoin;
double&ret=cache[upCoin][idx];
if(ret>-0.5)return ret;
ret=0.0;
int downCoin=N-upCoin;
//i:upCoin selected, j:downCoint selected
for(int i=0;i<=order[idx];i++)
{
int j=order[idx]-i;
if(downCoin<j||upCoin<i)continue;
ret+=f(upCoin-i+j,idx+1)*(comb(upCoin,i)*comb(downCoin,j))/comb(N,order[idx]);
}
return ret;
}
int main()
{
cin>>N>>K;
memset(cache,-1,sizeof(cache));
memset(cache2,-1,sizeof(cache2));
order.resize(K);
for(auto&i:order)cin>>i;
cout<<fixed;
cout.precision(9);
cout<<f(N,0);
}
확률 계산이 (comb(upCoin,i)*comb(downCoin,j))/comb(N,order[idx]) 로 까다로운 점을 제외하면
이전문제와 크게 다르지 않습니다.
하지만 모든문제에서 dp를 쓸수있는건 아닙니다.
https://www.acmicpc.net/problem/13347
13347번: Lost In The Woods
The first line contains two integers N and M, where N is the number of clearings in the woods (2 ≤ N ≤ 20), and M is the total number of paths between clearings. The clearings are numbered 0 through N − 1, such that clearing 0 is the one where your friend
www.acmicpc.net
다음문제와 같이 양방향그래프가 주어져있을때, 출발노드는0번노드이고, 도착노드는 N-1입니다.
노드 이동시간이 1일때, 도착노드에 도착하는 기댓값을 구하는문제입니다. 간단해보이는데, 이전과같은 접근법을
시도하면 루프의 늪에 빠지게 됩니다. 그리고 우리가 사용하던 재귀dp는 무한루프가 생겼을때, 대처를 못합니다.
함수인자에 depth를 추가해 몇만번 이상 depth가 누적되면 종료하는 방식도있지만, depth의 종료조건을 계산하기 까다롭고, depth의 길이만큼 메모이제이션의 크기도 엄청나게 불어날것이며 그에따라 메모리초과를 일으키거나 매우 비효율적으로 알고리즘이 동작할것입니다.
이를 해결하기위해, '확률의 이동'을 새로 생각해 봅시다.
예제 1
3 3
0 1
1 2
0 2
다음 그래프에서 (node번호,확률) 이라고했을때
초기그래프는 다음과 같이 둘 수 있습니다. 0번노드에 1.0확률이 있습니다.

여기서 1.0은 1/2확률로 1번노드로 이동을하고, 1/2확률로 2번노드로 이동을 합니다.
이동할때 해당확률에 1/2를 곱해줍시다.

2초일때의 상황입니다. 1번노드에 0.5확률이있고, 2번노드에 0.5확률이 있게되는데, 여기서 2번노드는 도착노드이므로
도착확률에 현재 시간을 곱해줍시다. (sum+=0.5*2) 그리고 1번노드의 0.5도 1/2확률로 0번노드로 이동을하고, 1/2확률로 2번노드로 이동을합니다.

3초일때의 상황입니다. 마찬가지로 2번노드에 0.25가 도착했으므로 (sum+=0.25*3)을 하면됩니다. 0번노드의 0.25는 또 1/2확률로 1,2번노드로 이동을하고....
를 반복해주면됩니다. 그리고 이를 구현해주면 됩니다.
#include <iostream>
#include <algorithm>
#include <string.h>
#include <vector>
using namespace std;
int n, m;
vector<int> adj[21];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<double> node(n, 0.0);
node[0] = 1.0;
double ret = 0.0;
// Each step:
for (int i = 1; i < 10000; i++)
{
vector<double> new_node(n, 0.0);
for (int u = 0; u < n; u++)
for (int v : adj[u])
new_node[v] += node[u] / adj[u].size();
ret += i * new_node[n - 1];
node = new_node;
node[n - 1] = 0.0;
}
cout << fixed;
cout.precision(8);
cout << ret;
}
1만번정도만 반복문을 돌면됩니다. 몇번정도 반복문을 돌아야하는지는 공식이있을텐데 아직 찾지는 못했습니다.
양방향그래프이므로 입력받을때 간선을 양방향으로 추가하는것도 잊지맙시다.
추천문제
복권 + 은행: https://www.acmicpc.net/problem/13258
13258번: 복권 + 은행
두 번째 예제의 경우에 첫 주가 지난 후 1/3의 확률로 (3, 2, 2)가, 1/3의 확률로 (2, 3, 2)가, 1/3의 확률로 (2, 2, 3)이 된다. 둘째 주에 (3, 2, 2)는 기댓값이 3.4286이 되고, (2, 3, 2)와 (2, 2, 3)은 기댓값이 2.2857이 된다. 따라서, 기댓값은 2.66667이다.
www.acmicpc.net
토끼의 이동: https://www.acmicpc.net/problem/13247
13247번: 토끼의 이동
첫째 줄에 게임판의 색상이 주어진다. 게임판의 크기(N)는 2보다 크거나 같고, 17보다 작거나 같으며, W는 흰색, B는 검정색, R은 빨간색을 나타낸다. 둘째 줄에는 토끼의 수 r (1 ≤ r ≤ N)이 주어진다.
www.acmicpc.net
랜덤 소트:https://www.acmicpc.net/problem/1521
1521번: 랜덤 소트
첫째 줄에 순열의 크기 N이 주어진다. 둘째 줄에 순열에 들어있는 수 N개가 주어진다. 이 수는 모두 1보다 크거나 같고, N보나 작거나 같으며, 같은 수는 2번 이상 주어지지 않는다. 또, N은 8보다 작거나 같은 자연수이다.
www.acmicpc.net
Following Flow:https://www.acmicpc.net/problem/10894
10894번: Following Flow
세상은 N+1개의 정점으로 이루어져 있는데, 각 정점은 0에서 N까지의 번호가 붙어있다. 각 정점에서는 다른 정점으로 가는 간선이 있는데, 각 간선은 일방통행이며, 각 간선마다 간선을 지나가는데 걸리는 시간이 다르다. 동현이는 세상을 떠돌고 있는데, 0번 지점은 동현이가 현재 있는 위치이고, N번은 동현이의 집이다. 동현이는 집에 도착하기 전까지는 마음이 가는 대로 세상을 떠돌고 싶어한다. 마음이 가는 대로라는 것은 현재 정점에서 다른 정점으로 갈 수 있
www.acmicpc.net
Research Productivity Index:https://www.acmicpc.net/problem/17591
17591번: Research Productivity Index
The first line of the input has a single integer n (1 ≤ n ≤ 100), the number of Angela’s candidate papers. The next line has n space-separated integers giving the probability of each paper getting accepted. Each probability value is given as an integer per
www.acmicpc.net
랜덤 걷기:https://www.acmicpc.net/problem/3946
3946번: 랜덤 걷기
문제 걷기 전에 동전을 던진 다음, 앞 면이면 왼쪽으로 한 칸, 뒷 면이면 오른쪽으로 한 칸 이동하는 방법을 랜덤 걷기라고 한다. 이 랜덤 걷기의 위치의 기댓값은 항상 0이 된다. 즉, 랜덤 걷기를 아무리 많이 한다고 해도, 평균 위치는 처음 시작한 지점과 같다. 랜덤 걷기에서 왼쪽으로 갈 확률과 오른쪽으로 갈 확률, 그리고 동전을 던지는 횟수가 주어졌을 때, 가장 오른쪽 위치의 기댓값을 구하는 프로그램을 작성하시오. 입력 첫째 줄에는 테스트 케이스의 P
www.acmicpc.net
'👨💻코드 포스터' 카테고리의 다른 글
| 코테 준비 알고리즘 - 정렬 (0) | 2021.04.27 |
|---|---|
| 게임 이론(스프라그-그런디 이론) (0) | 2020.04.27 |
| Heavy-Light Decomposition 알고리즘 (0) | 2020.01.28 |
