항상 백준에서 다른 대학교들이 내부 알고리즘 대회 개최하는 걸 부러워했고, 또 아쉬워했는데 우리 학교 과학생회가 노력해주신 덕분에 처음이자 마지막이 될 알고리즘 대회를 잘 치렀습니다. 풀이를 지난주 내부 대회가 끝난 당일 바로 올리려 했는데 생각해보니 10월 14일에 백준 오픈 대회가 열리는 터라, 끝나고 올립니다.
사실 백준을 안 푼지도 거의 1~2년이고 대회는 거진 3년 만이라 시작하기 전엔 솔직히 조금 불안했는데, 올 솔브를 달성해서 뿌듯합니다.
간단한 풀이과정과 내용을 공유해드립니다.
A. 거울반사
간단한 브론즈 구현문제입니다. 2와 5의 좌우반전만 생각했다가 삽질하고 상하반전을 추가하고 맞았던 문제입니다.
A번 틀리니까 당황하고 BCDE 풀고 다시 보니 틀린 점이 보였던 문제였습니다. 이 방식은 기업 코테에도 유효한데, 틀려서 막혔다고 무조건 잡고 있으면 시간만 흘러갈 가능성이 높습니다. 의외로 다른 문제를 풀고 가벼운 마음으로 다시 보면 새로운 무언가가 보일 때가 있습니다.
#include <iostream>
using namespace std;
int left_right[12]= {0,1,5,-1,-1,2,-1,-1,8,-1};
int up_down[12]= {0,1,5,-1,-1,2,-1,-1,8,-1};
int arr[50][50];
int main(){
char type;
int N;
cin>>type>>N;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++) cin>>arr[i][j];
if(type=='U' || type=='D'){
for(int i=N-1;i>=0;i--,cout<<"\n")
for(int j=0;j<N;j++,cout<<' '){
if(up_down[arr[i][j]]==-1) cout<<'?';
else cout<<up_down[arr[i][j]];
}
}
else{
for(int i=0;i<N;i++,cout<<"\n")
for(int j=N-1;j>=0;j--,cout<<' '){
if(left_right[arr[i][j]]==-1) cout<<'?';
else cout<<left_right[arr[i][j]];
}
}
}
B. 방어율 무시 계산하기
역시 간단한 브론즈 구현 문제입니다. double형과 부동소수점을 다룰 줄 아는지 물어보려고 했던 것 같네요.
#include <vector>
#include <iostream>
using namespace std;
int main(){
int N;
cin>>N;
vector<int>v(N);
for(auto&i : v)cin>>i;
double now = 0.0;
cout<<fixed;
cout.precision(7);
for(auto i: v){
now = 1.0-(1.0-now)*(1.0-(double)i/100);
cout<<now*100<<" ";
}
}
C. 임스와 함께하는 미니게임
간단한 실버 자료구조 활용 문제입니다. 중복된 문자열을 처리하는 데에 Set 자료구조가 떠올라야 합니다. Map 자료구조도 가능하나 Key-Value형은 필요가 없기 때문에 꼭 들어맞지는 않습니다. Set은 균형 잡힌 이진트리 형으로, 삽입 및 탐색에 최대 O(logN)이 소요됩니다. 다만 여기서 문자열을 넣고 꼭 정렬을 할 필요는 없으므로 C++의 해시 맵 자료구조인 unordered_map을 사용하면 더 빠른 시간에 동작할 수 있습니다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
int main(){
set<string> st;
int N;
char type;
cin>>N>>type;
for(int i=0;i<N;i++){
string s;
cin>>s;
st.insert(s);
}
if(type=='Y') cout<<(st.size())/1;
else if(type=='F') cout<<(st.size())/2;
else cout<<(st.size())/3;
}
D. 유전자 조합
자료구조 응용형 문제입니다. 그리고 시간복잡도 계산과 예외 케이스 처리가 필요한 문제입니다. 먼저 N의 크기가 몇 만이므로 모든 문자열을 탐색하면서 유전자를 생성하는 방법은 시간 초과가 납니다. O(N*N) 이기에 몇 만의 제곱이 되어 10억 번의 연산을 넘게 되죠.
이 시간 복잡도를 줄이기 위해선 N의 크기는()만 이지만 그 문자열은 중복이 포함될 수 있다는 점에 주목해야 합니다. 문자열은 2개의 문자로 이루어져 있고, 그 문자는 모두 'A'~'Z' = 27개이니 조합될 수 있는 문자열의 개수는 최대 27*27=729개입니다. 따라서 1만 개의 문자열이 주어져도 최대 729개로 압축시킬 수 있다는 이야기입니다. (중복을 제거하니)
문자열을 제거해주기 위해 앞서 등장했던 set을 사용해주고, 답을 담을 때도 중복을 제거해주기 위해 set을 또 사용해줍니다.
이렇게 문제를 풀어주면 맞을 것 같으나... 예외 케이스가 하나 있습니다.
2
AA AA
다음과 같은 경우는 답이 1 A 가되어야 하지만, 우리는 중복을 모두 제거해준 덕분에 AA 문자열 하나만 있다고 생각하고 0이라는 답을 뱉습니다. 즉, 2번 이상 등장한 문자열은 자기 자신과도 짝을 지어줘야 합니다. 이를 위해 twice라는 이름의 set 자료구조를 하나 만들고, 이미 등장한 문자열이라면 2번 이상 등장하는 문자열이라는 의미이니 twice 이름의 set에 넣어줍니다. 이후 유전자 교배를 하는 과정에서 두 번 등장한 문자열은 자기 자신과 짝을 맺도록 해주면 무사히 예외 케이스를 처리할 수 있습니다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
set<string> twice;
int main(){
set<string> st;
int N;
cin>>N;
for(int i=0;i<N;i++){
string s;
cin>>s;
if(st.find(s)!=st.end()) twice.insert(s);
else st.insert(s);
}
vector<string>v;
for(auto i:st) v.push_back(i);
set<char> ans;
for(int i=0;i<v.size();i++)
for(int j=0;j<v.size();j++){
if(i==j && twice.find(v[i]) == twice.end()) continue;
char a = v[i][0], b = v[j][1];
ans.insert(max(a,b));
}
cout<<ans.size()<<"\n";
for(auto c:ans) cout<<c<<" ";
}
E. 들판 건너가기
간단한 DP 기본형 문제입니다. DP를 처음부터 설명하기엔 너무 길지만 공부를 하신 분이라면 모두 무난히 푸실 만한 기본 문제입니다. DP 테이블을 [현재 idx][마지막으로 고른 물건의 가치] 로 가져가면 풀 수 있습니다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
int N;
vector<int> arr;
int cache[100000+2][100+2];
int f(int idx,int last){
if(idx==N)return 0;
int&ret=cache[idx][last];
if(ret!=-1) return ret;
if(last==0) return ret = max(f(idx+1,last),f(idx+1,arr[idx]));
else return ret= max(f(idx+1,last),f(idx+1,arr[idx])+(arr[idx]-last)*(arr[idx]-last));
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin>>N;
arr.resize(N);
memset(cache,-1,sizeof(cache));
for(auto&i:arr)cin>>i;
cout<<f(0,0);
}
F. 귀경길 교통상황을 알려드립니다
약간의 생각의 전환이 필요한 문제입니다. 우선 문제에서 언급하진 않았지만 노드의 개수가 N, 간선의 개수가 N-1이므로 트리구조임을 바로 캐치해야 합니다. 따라서 트리의 루트로 향하는 차들이 소요되는 시간을 계산해야 하는 건데... 이를 그대로 시뮬레이션을 구현하기엔 까다롭고 시간 복잡도도 크므로 곤란합니다. 부모 노드로 향하는 차들.. 대기도 구현을 해야 하고, 노드에 모두 차들이 차있다면 시간 초과도 뻔한 일입니다.
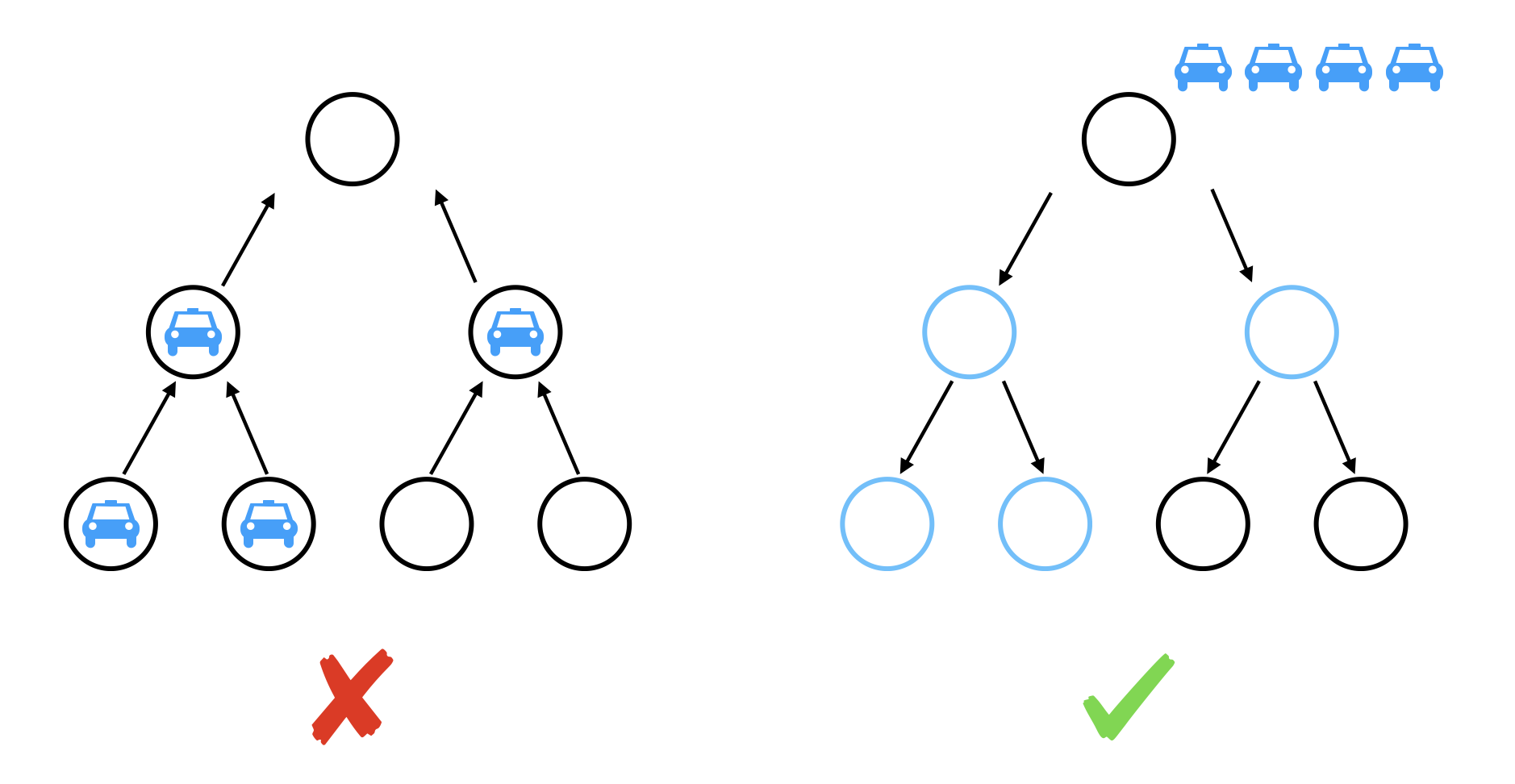
역으로 생각해봅시다. 트리가 모두 텅 비어있고, 루트 노드에서부터 차들 각각을 각자의 목적지로 출발시키는 걸로요. 이렇게 생각하면 루트 노드로부터 가장 멀리 떨어져 있는 목적지로 가는 차부터 쏘는 것이 이득임을 알 수 있습니다. 뿐만 아니라 사이클이 없고 노드-노드 경로가 유일한 트리의 특성상, 먼저 출발시킨 차가 뒤에 출발시킨 차의 진로를 방해하는 일조차 없음을 알 수 있습니다. 또 목적지로의 경로의 길이가 같은 차가 여러 대 있더라도, 어떤 차를 먼저 출발시키든 행위의 결괏값은 같습니다. 정리하자면 결국 앞이 막혀있어 대기하는 문제의 상황을 역으로 생각해 먼저 출발한 차가 대기하는 것이 되는 것이죠.
그러니 우리가 해야 할 일은, 루트 노드로부터 차의 도착지까지의 길이를 모두 저장하고, 내림차순으로 정렬시켜 그 순서대로 차들을 출발시키는 겁니다. 트리구조에서 루트노드로 부터 거리를 구하는 방법은 너무 클래식하죠. dfs나 bfs를 사용하면 됩니다.
그럼 도착지까지의 길이를 구했다면, 모든 차들이 목적지에 도착하는 시간을 어떻게 구할 수 있을까요? 먼저 과정들을 시뮬레이션해봅시다.
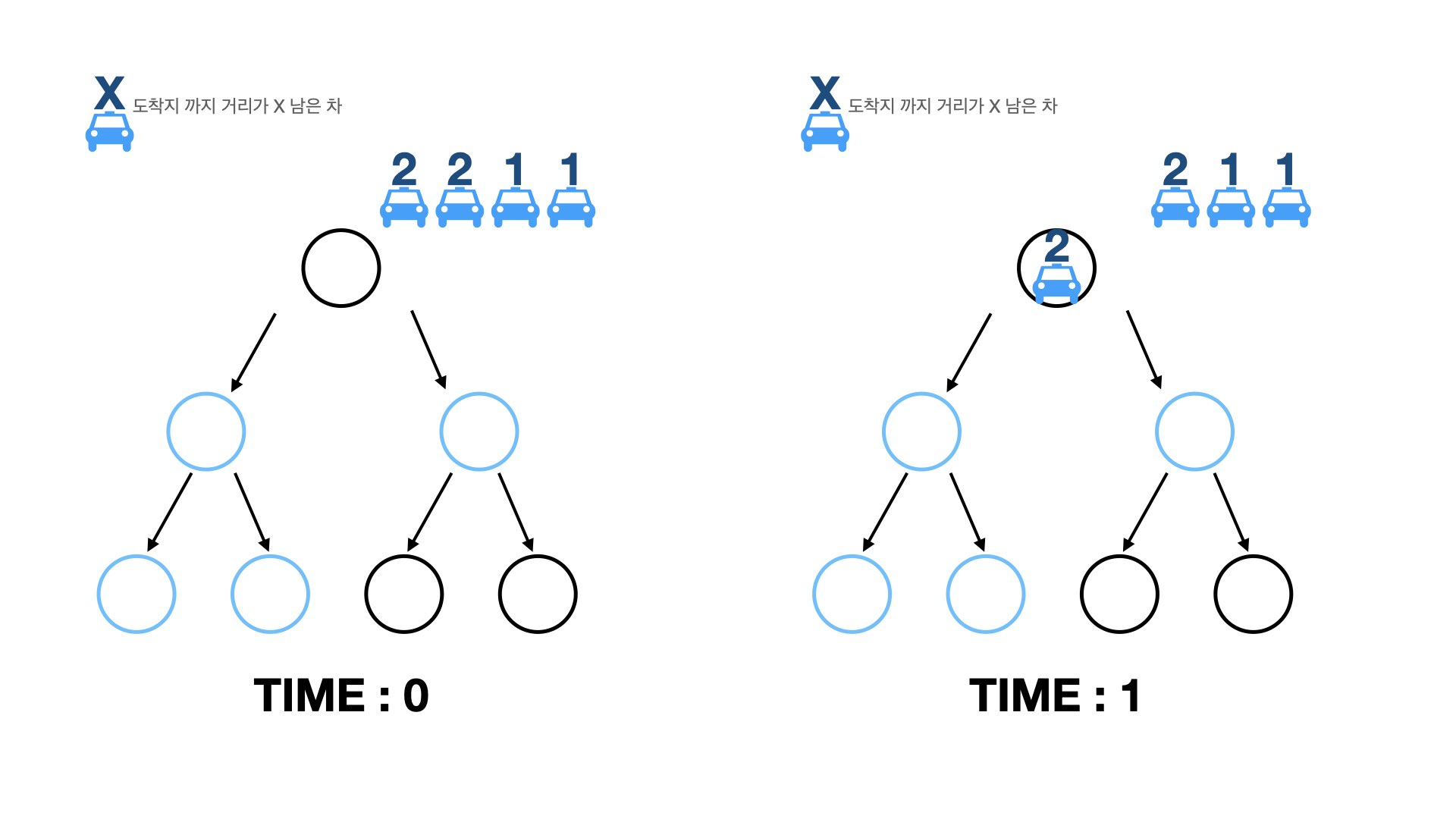
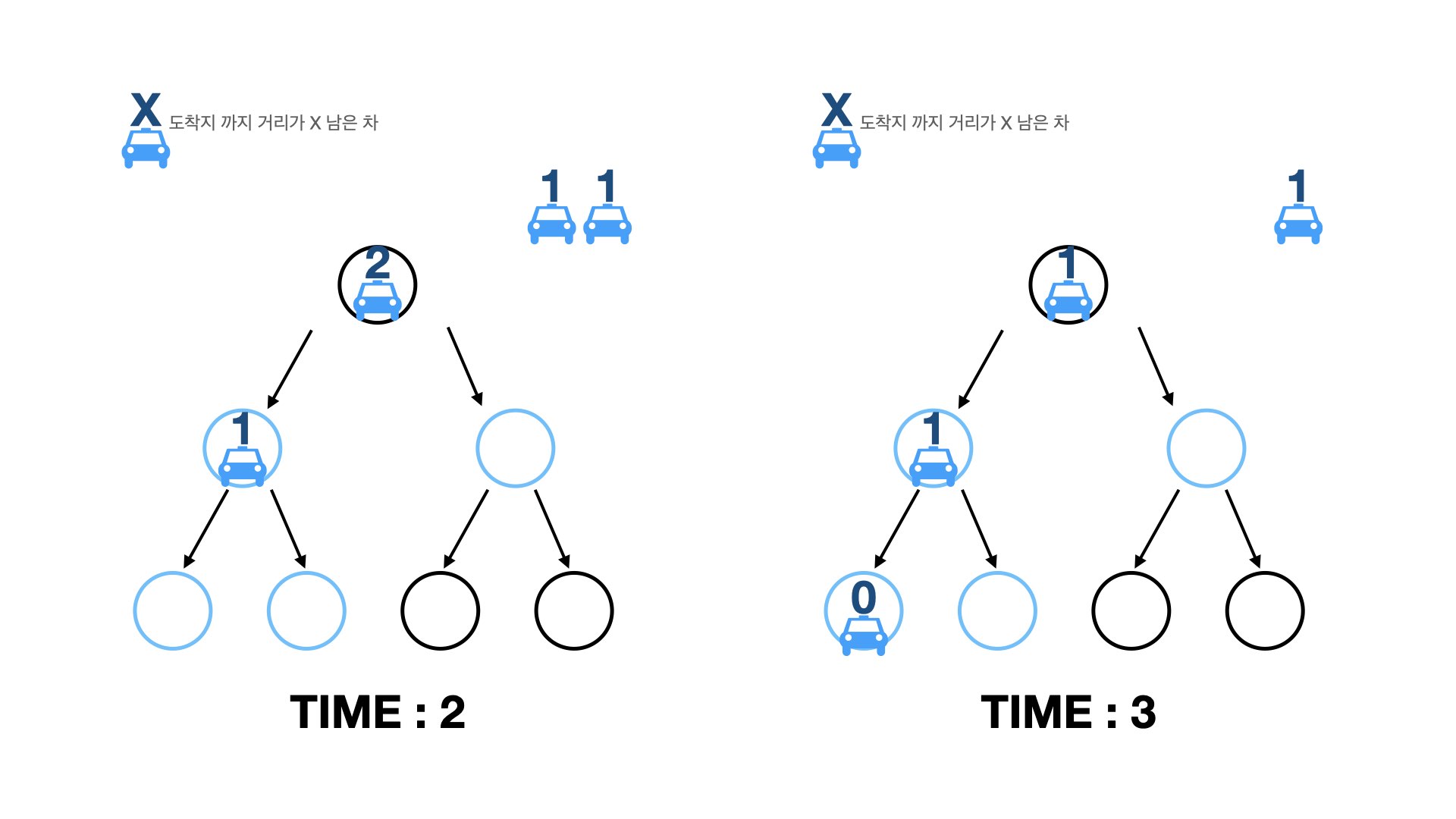
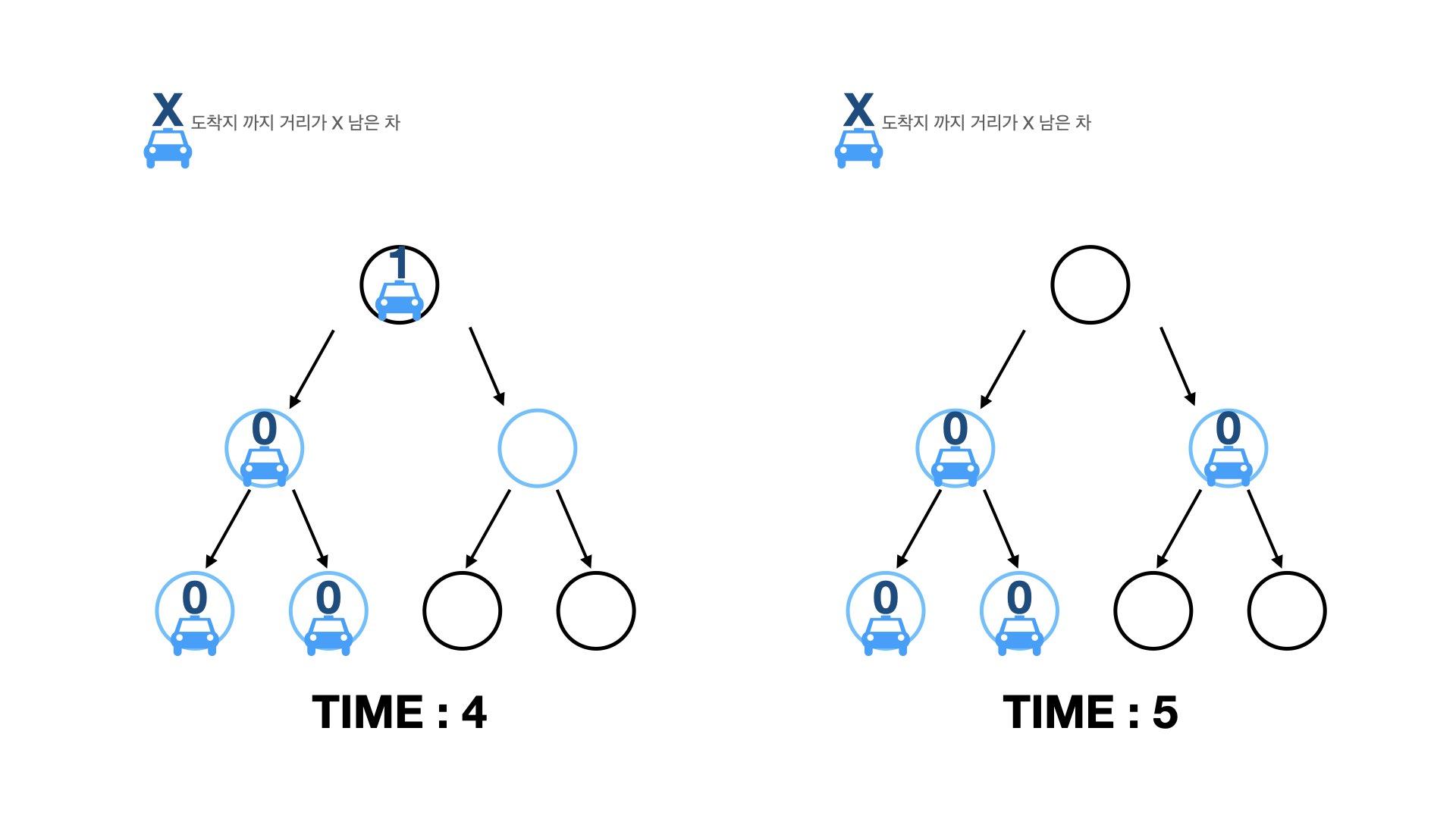
과정들을 보니, 다음과 같이 정리할 수 있습니다.
- 대기하고 있는 차들을 차들의 이동거리(도착지까지의 거리)의 내림차순으로 대기시킨다.
- 매 시간마다 차들을 루트 노드에서부터 순서대로 내보낸다.
- 결국, 각 차들의 이동시간은 (대기시간)+(도착지까지의 거리)이다.
- 그러므로, 정답은 3번에서 도출된 각 차들의 이동시간의 최댓값이다.
코드로 이를 구현하면 다음과 같습니다.
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int MAX_N=200000+2;
int N;
vector<int>adj[MAX_N];
bool in_car[MAX_N]={0,};
int visited[MAX_N]={0,};
void bfs(int start){
queue<int>q;
visited[start]=true;
q.push(start);
while(!q.empty()){
int now=q.front();
q.pop();
for(auto next:adj[now]){
if(visited[next]) continue;
visited[next]=visited[now]+1;
q.push(next);
}
}
return ;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin>>N;
for(int i=0;i<N-1;i++){
int u,v;
cin>>u>>v;
adj[u].push_back(v);
adj[v].push_back(u);
}
for(int i=0;i<N;i++){
bool flag;
cin>>flag;
in_car[i+1]=flag;
}
bfs(1);
vector<int>arr;
for(int i=1;i<=N;i++){
if(in_car[i]) arr.push_back(visited[i]);
}
sort(arr.rbegin(),arr.rend());
int time=0,maxN=0;
for(auto i:arr){
maxN=max(maxN,i+time);
time++;
}
cout<<maxN;
}
G. 축사 건설
대망의 올 솔브 방지 문제입니다. 축사의 크기가 2000*2000으로 매우 크고, 쿼리도 10만 개나 주어지니 매번 쿼리마다 해당 크기의 직사각형이 있는지를 반복문으로 찾으면 O(쿼리의 개수 * 축사의 크기 * 쿼리의 직사각형 크기)가 되어 시간 복잡도의 크기가 우주를 넘어버립니다. 쿼리가 들어올 때마다 답을 찾는 것이 아닌, 미리 답을 구해놓고 배열에 저장해두어 필요할 때마다 꺼내서 사용하면 쉬울 것 같다는 예감이 들지 않나요?
그러니까, 가로의 길이가 N일 때에 가질 수 있는 세로 값의 최댓값을 저장해둔 maxX[N] 배열만 빠르게 구할 수 있다면, maxX[N]보다 큰 값은 실패, 이하인 값은 성공으로 줄 수 있겠다는 것입니다. 그러면 또 maxX[N] 배열을 어떻게 빠르게 구할 수 있을까요?
히스토그램에서 가장 큰 직사각형 문제를 기억하시나요? 해당 문제를 푸는 여러 방법이 있지만, 그중 가장 시간 복잡도가 낮은 방법은 스택을 사용한 그리디 알고리즘을 활용하는 방법입니다. 이 방법은 매우 유명하고 풀이를 설명한 블로그들이 많으니 설명은 생략하겠습니다. 다만 이 문제를 풀기 위해선 해당 풀이에 대한 이해가 필수입니다.
그럼 이제부터 우리가 사용할 방법은 맨 위의 가로행부터 히스토그램을 만들어가고, 그 히스토그램에서 가장 큰 직사각형을 만드는 문제를 풀 겁니다.
맨 위의 가로행부터 맨 아래의 가로행까지 진행하면서 총가로의 길이(R)만큼 히스토그램을 만드니, 시간 복잡도는 O(R*C)가 됩니다. 스택을 사용한 히스토그램에서 가장 큰 직사각형 문제를 푸는 시간복잡도는 O(C)이니까요.
히스토그램을 맨 위의 가로행부터 만드는 방법은 다음과 같습니다.
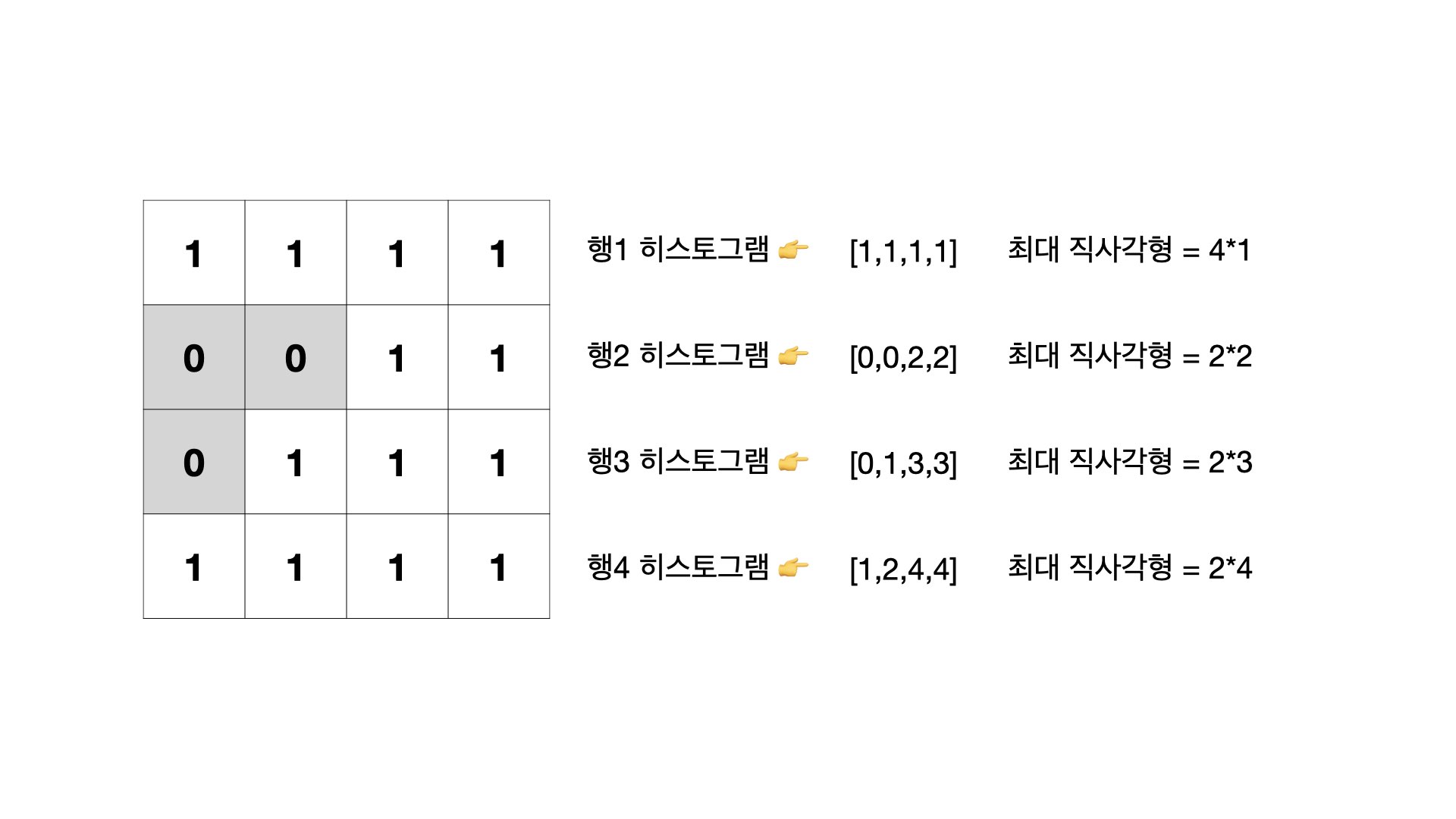
위의 행의 값을 더해가는데, 만약 해당 행의 칸의 값이 0이라면 0 값을 취하면서 진행합니다. 히스토그램을 구했다면 앞서 말한 스택으로 푸는 히스토그램에서 가장 큰 직사각형 문제를 푸면 됩니다. 코드로 확인해볼까요?
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
int R,C;
int arr[2002][2002] = {};
vector<int>maxX(2002,0);
void histogram(int row[])
{
stack<int> ret;
int top_val;
int area = 0;
int idx = 0;
while (idx < C) {
if (ret.empty() || row[ret.top()] <= row[idx])
ret.push(idx++);
else {
top_val = row[ret.top()];
ret.pop();
if (!ret.empty()){
area = top_val * (idx - ret.top() - 1);
maxX[top_val]=max(maxX[top_val],(idx - ret.top() - 1));
}else{
area = top_val * idx;
maxX[top_val]=max(maxX[top_val],idx);
}
}
}
while (!ret.empty()) {
top_val = row[ret.top()];
ret.pop();
if (!ret.empty()){
area = top_val * (idx - ret.top() - 1);
maxX[top_val]=max(maxX[top_val],(idx - ret.top() - 1));
}else{
area = top_val * idx;
maxX[top_val]=max(maxX[top_val],idx);
}
}
return;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cin>>R>>C;
for(int i=0;i<R;i++){
string s;
cin>>s;
for(int j=0;j<C;j++){
arr[i][j]=(s[j]=='.'? 1:0);
}
}
for (int i=1;i<R;i++) {
for (int j=0;j<C;j++){
if (arr[i][j]) arr[i][j]+=arr[i-1][j];
}
histogram(arr[i]);
}
//for(int i=1;i<=6;i++)cout<<i<<"*"<<maxX[i]<<endl;
int Q;
cin>>Q;
while(Q--){
int a,b;
cin>>a>>b;
if(b<=maxX[a])cout<<"YES\n";
else cout<<"NO\n";
}
return 0;
}
풀이는 여기까지입니다. 대회 알고리즘을 접은 이유라는 글도 적었긴 했는데, 그럼에도 알고리즘은 도전할만한 가치가 충분하고 저희 학교의 학우 분들도 PS에 많은 관심이 생겼으면 좋겠습니다. 그러기에 이번 첫 교내 알고리즘 대회가 의미가 뜻깊습니다. 다시 한번 수고한 학생회와 출제진, 검수진 분들에게 박수 쳐주고 싶습니다. 고생 많으셨습니다.
내가 대회 알고리즘을 접은 이유
안녕하세요. 오랜만의 일상 글입니다. 최근 블로그에 개발 글만 올라와서 내가 봐도 재미가 없어 보이기도 하고 해서, 대회 알고리즘에 관해 제 생각을 조금 적어 두려 합니다. 우선 저는 대회
newdeal123.tistory.com
내년에는 졸업생이니, 기회가 된다면 출제진으로 만나 뵙겠습니다.
P.S. 알고리즘이나 개발에 관심 있어 저희 교내 학과 동아리인 NL 에 입부를 희망하시는 분은 비공개 댓글 달아주시길 바랍니다. 언제든 환영입니다..! ☺️
항상 백준에서 다른 대학교들이 내부 알고리즘 대회 개최하는 걸 부러워했고, 또 아쉬워했는데 우리 학교 과학생회가 노력해주신 덕분에 처음이자 마지막이 될 알고리즘 대회를 잘 치렀습니다. 풀이를 지난주 내부 대회가 끝난 당일 바로 올리려 했는데 생각해보니 10월 14일에 백준 오픈 대회가 열리는 터라, 끝나고 올립니다.
사실 백준을 안 푼지도 거의 1~2년이고 대회는 거진 3년 만이라 시작하기 전엔 솔직히 조금 불안했는데, 올 솔브를 달성해서 뿌듯합니다.
간단한 풀이과정과 내용을 공유해드립니다.
A. 거울반사
간단한 브론즈 구현문제입니다. 2와 5의 좌우반전만 생각했다가 삽질하고 상하반전을 추가하고 맞았던 문제입니다.
A번 틀리니까 당황하고 BCDE 풀고 다시 보니 틀린 점이 보였던 문제였습니다. 이 방식은 기업 코테에도 유효한데, 틀려서 막혔다고 무조건 잡고 있으면 시간만 흘러갈 가능성이 높습니다. 의외로 다른 문제를 풀고 가벼운 마음으로 다시 보면 새로운 무언가가 보일 때가 있습니다.
#include <iostream>
using namespace std;
int left_right[12]= {0,1,5,-1,-1,2,-1,-1,8,-1};
int up_down[12]= {0,1,5,-1,-1,2,-1,-1,8,-1};
int arr[50][50];
int main(){
char type;
int N;
cin>>type>>N;
for(int i=0;i<N;i++)
for(int j=0;j<N;j++) cin>>arr[i][j];
if(type=='U' || type=='D'){
for(int i=N-1;i>=0;i--,cout<<"\n")
for(int j=0;j<N;j++,cout<<' '){
if(up_down[arr[i][j]]==-1) cout<<'?';
else cout<<up_down[arr[i][j]];
}
}
else{
for(int i=0;i<N;i++,cout<<"\n")
for(int j=N-1;j>=0;j--,cout<<' '){
if(left_right[arr[i][j]]==-1) cout<<'?';
else cout<<left_right[arr[i][j]];
}
}
}
B. 방어율 무시 계산하기
역시 간단한 브론즈 구현 문제입니다. double형과 부동소수점을 다룰 줄 아는지 물어보려고 했던 것 같네요.
#include <vector>
#include <iostream>
using namespace std;
int main(){
int N;
cin>>N;
vector<int>v(N);
for(auto&i : v)cin>>i;
double now = 0.0;
cout<<fixed;
cout.precision(7);
for(auto i: v){
now = 1.0-(1.0-now)*(1.0-(double)i/100);
cout<<now*100<<" ";
}
}
C. 임스와 함께하는 미니게임
간단한 실버 자료구조 활용 문제입니다. 중복된 문자열을 처리하는 데에 Set 자료구조가 떠올라야 합니다. Map 자료구조도 가능하나 Key-Value형은 필요가 없기 때문에 꼭 들어맞지는 않습니다. Set은 균형 잡힌 이진트리 형으로, 삽입 및 탐색에 최대 O(logN)이 소요됩니다. 다만 여기서 문자열을 넣고 꼭 정렬을 할 필요는 없으므로 C++의 해시 맵 자료구조인 unordered_map을 사용하면 더 빠른 시간에 동작할 수 있습니다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
int main(){
set<string> st;
int N;
char type;
cin>>N>>type;
for(int i=0;i<N;i++){
string s;
cin>>s;
st.insert(s);
}
if(type=='Y') cout<<(st.size())/1;
else if(type=='F') cout<<(st.size())/2;
else cout<<(st.size())/3;
}
D. 유전자 조합
자료구조 응용형 문제입니다. 그리고 시간복잡도 계산과 예외 케이스 처리가 필요한 문제입니다. 먼저 N의 크기가 몇 만이므로 모든 문자열을 탐색하면서 유전자를 생성하는 방법은 시간 초과가 납니다. O(N*N) 이기에 몇 만의 제곱이 되어 10억 번의 연산을 넘게 되죠.
이 시간 복잡도를 줄이기 위해선 N의 크기는()만 이지만 그 문자열은 중복이 포함될 수 있다는 점에 주목해야 합니다. 문자열은 2개의 문자로 이루어져 있고, 그 문자는 모두 'A'~'Z' = 27개이니 조합될 수 있는 문자열의 개수는 최대 27*27=729개입니다. 따라서 1만 개의 문자열이 주어져도 최대 729개로 압축시킬 수 있다는 이야기입니다. (중복을 제거하니)
문자열을 제거해주기 위해 앞서 등장했던 set을 사용해주고, 답을 담을 때도 중복을 제거해주기 위해 set을 또 사용해줍니다.
이렇게 문제를 풀어주면 맞을 것 같으나... 예외 케이스가 하나 있습니다.
2
AA AA
다음과 같은 경우는 답이 1 A 가되어야 하지만, 우리는 중복을 모두 제거해준 덕분에 AA 문자열 하나만 있다고 생각하고 0이라는 답을 뱉습니다. 즉, 2번 이상 등장한 문자열은 자기 자신과도 짝을 지어줘야 합니다. 이를 위해 twice라는 이름의 set 자료구조를 하나 만들고, 이미 등장한 문자열이라면 2번 이상 등장하는 문자열이라는 의미이니 twice 이름의 set에 넣어줍니다. 이후 유전자 교배를 하는 과정에서 두 번 등장한 문자열은 자기 자신과 짝을 맺도록 해주면 무사히 예외 케이스를 처리할 수 있습니다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <set>
using namespace std;
set<string> twice;
int main(){
set<string> st;
int N;
cin>>N;
for(int i=0;i<N;i++){
string s;
cin>>s;
if(st.find(s)!=st.end()) twice.insert(s);
else st.insert(s);
}
vector<string>v;
for(auto i:st) v.push_back(i);
set<char> ans;
for(int i=0;i<v.size();i++)
for(int j=0;j<v.size();j++){
if(i==j && twice.find(v[i]) == twice.end()) continue;
char a = v[i][0], b = v[j][1];
ans.insert(max(a,b));
}
cout<<ans.size()<<"\n";
for(auto c:ans) cout<<c<<" ";
}
E. 들판 건너가기
간단한 DP 기본형 문제입니다. DP를 처음부터 설명하기엔 너무 길지만 공부를 하신 분이라면 모두 무난히 푸실 만한 기본 문제입니다. DP 테이블을 [현재 idx][마지막으로 고른 물건의 가치] 로 가져가면 풀 수 있습니다.
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
int N;
vector<int> arr;
int cache[100000+2][100+2];
int f(int idx,int last){
if(idx==N)return 0;
int&ret=cache[idx][last];
if(ret!=-1) return ret;
if(last==0) return ret = max(f(idx+1,last),f(idx+1,arr[idx]));
else return ret= max(f(idx+1,last),f(idx+1,arr[idx])+(arr[idx]-last)*(arr[idx]-last));
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin>>N;
arr.resize(N);
memset(cache,-1,sizeof(cache));
for(auto&i:arr)cin>>i;
cout<<f(0,0);
}
F. 귀경길 교통상황을 알려드립니다
약간의 생각의 전환이 필요한 문제입니다. 우선 문제에서 언급하진 않았지만 노드의 개수가 N, 간선의 개수가 N-1이므로 트리구조임을 바로 캐치해야 합니다. 따라서 트리의 루트로 향하는 차들이 소요되는 시간을 계산해야 하는 건데... 이를 그대로 시뮬레이션을 구현하기엔 까다롭고 시간 복잡도도 크므로 곤란합니다. 부모 노드로 향하는 차들.. 대기도 구현을 해야 하고, 노드에 모두 차들이 차있다면 시간 초과도 뻔한 일입니다.

역으로 생각해봅시다. 트리가 모두 텅 비어있고, 루트 노드에서부터 차들 각각을 각자의 목적지로 출발시키는 걸로요. 이렇게 생각하면 루트 노드로부터 가장 멀리 떨어져 있는 목적지로 가는 차부터 쏘는 것이 이득임을 알 수 있습니다. 뿐만 아니라 사이클이 없고 노드-노드 경로가 유일한 트리의 특성상, 먼저 출발시킨 차가 뒤에 출발시킨 차의 진로를 방해하는 일조차 없음을 알 수 있습니다. 또 목적지로의 경로의 길이가 같은 차가 여러 대 있더라도, 어떤 차를 먼저 출발시키든 행위의 결괏값은 같습니다. 정리하자면 결국 앞이 막혀있어 대기하는 문제의 상황을 역으로 생각해 먼저 출발한 차가 대기하는 것이 되는 것이죠.
그러니 우리가 해야 할 일은, 루트 노드로부터 차의 도착지까지의 길이를 모두 저장하고, 내림차순으로 정렬시켜 그 순서대로 차들을 출발시키는 겁니다. 트리구조에서 루트노드로 부터 거리를 구하는 방법은 너무 클래식하죠. dfs나 bfs를 사용하면 됩니다.
그럼 도착지까지의 길이를 구했다면, 모든 차들이 목적지에 도착하는 시간을 어떻게 구할 수 있을까요? 먼저 과정들을 시뮬레이션해봅시다.



과정들을 보니, 다음과 같이 정리할 수 있습니다.
- 대기하고 있는 차들을 차들의 이동거리(도착지까지의 거리)의 내림차순으로 대기시킨다.
- 매 시간마다 차들을 루트 노드에서부터 순서대로 내보낸다.
- 결국, 각 차들의 이동시간은 (대기시간)+(도착지까지의 거리)이다.
- 그러므로, 정답은 3번에서 도출된 각 차들의 이동시간의 최댓값이다.
코드로 이를 구현하면 다음과 같습니다.
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int MAX_N=200000+2;
int N;
vector<int>adj[MAX_N];
bool in_car[MAX_N]={0,};
int visited[MAX_N]={0,};
void bfs(int start){
queue<int>q;
visited[start]=true;
q.push(start);
while(!q.empty()){
int now=q.front();
q.pop();
for(auto next:adj[now]){
if(visited[next]) continue;
visited[next]=visited[now]+1;
q.push(next);
}
}
return ;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin>>N;
for(int i=0;i<N-1;i++){
int u,v;
cin>>u>>v;
adj[u].push_back(v);
adj[v].push_back(u);
}
for(int i=0;i<N;i++){
bool flag;
cin>>flag;
in_car[i+1]=flag;
}
bfs(1);
vector<int>arr;
for(int i=1;i<=N;i++){
if(in_car[i]) arr.push_back(visited[i]);
}
sort(arr.rbegin(),arr.rend());
int time=0,maxN=0;
for(auto i:arr){
maxN=max(maxN,i+time);
time++;
}
cout<<maxN;
}
G. 축사 건설
대망의 올 솔브 방지 문제입니다. 축사의 크기가 2000*2000으로 매우 크고, 쿼리도 10만 개나 주어지니 매번 쿼리마다 해당 크기의 직사각형이 있는지를 반복문으로 찾으면 O(쿼리의 개수 * 축사의 크기 * 쿼리의 직사각형 크기)가 되어 시간 복잡도의 크기가 우주를 넘어버립니다. 쿼리가 들어올 때마다 답을 찾는 것이 아닌, 미리 답을 구해놓고 배열에 저장해두어 필요할 때마다 꺼내서 사용하면 쉬울 것 같다는 예감이 들지 않나요?
그러니까, 가로의 길이가 N일 때에 가질 수 있는 세로 값의 최댓값을 저장해둔 maxX[N] 배열만 빠르게 구할 수 있다면, maxX[N]보다 큰 값은 실패, 이하인 값은 성공으로 줄 수 있겠다는 것입니다. 그러면 또 maxX[N] 배열을 어떻게 빠르게 구할 수 있을까요?
히스토그램에서 가장 큰 직사각형 문제를 기억하시나요? 해당 문제를 푸는 여러 방법이 있지만, 그중 가장 시간 복잡도가 낮은 방법은 스택을 사용한 그리디 알고리즘을 활용하는 방법입니다. 이 방법은 매우 유명하고 풀이를 설명한 블로그들이 많으니 설명은 생략하겠습니다. 다만 이 문제를 풀기 위해선 해당 풀이에 대한 이해가 필수입니다.
그럼 이제부터 우리가 사용할 방법은 맨 위의 가로행부터 히스토그램을 만들어가고, 그 히스토그램에서 가장 큰 직사각형을 만드는 문제를 풀 겁니다.
맨 위의 가로행부터 맨 아래의 가로행까지 진행하면서 총가로의 길이(R)만큼 히스토그램을 만드니, 시간 복잡도는 O(R*C)가 됩니다. 스택을 사용한 히스토그램에서 가장 큰 직사각형 문제를 푸는 시간복잡도는 O(C)이니까요.
히스토그램을 맨 위의 가로행부터 만드는 방법은 다음과 같습니다.

위의 행의 값을 더해가는데, 만약 해당 행의 칸의 값이 0이라면 0 값을 취하면서 진행합니다. 히스토그램을 구했다면 앞서 말한 스택으로 푸는 히스토그램에서 가장 큰 직사각형 문제를 푸면 됩니다. 코드로 확인해볼까요?
#include <string>
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
int R,C;
int arr[2002][2002] = {};
vector<int>maxX(2002,0);
void histogram(int row[])
{
stack<int> ret;
int top_val;
int area = 0;
int idx = 0;
while (idx < C) {
if (ret.empty() || row[ret.top()] <= row[idx])
ret.push(idx++);
else {
top_val = row[ret.top()];
ret.pop();
if (!ret.empty()){
area = top_val * (idx - ret.top() - 1);
maxX[top_val]=max(maxX[top_val],(idx - ret.top() - 1));
}else{
area = top_val * idx;
maxX[top_val]=max(maxX[top_val],idx);
}
}
}
while (!ret.empty()) {
top_val = row[ret.top()];
ret.pop();
if (!ret.empty()){
area = top_val * (idx - ret.top() - 1);
maxX[top_val]=max(maxX[top_val],(idx - ret.top() - 1));
}else{
area = top_val * idx;
maxX[top_val]=max(maxX[top_val],idx);
}
}
return;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cin>>R>>C;
for(int i=0;i<R;i++){
string s;
cin>>s;
for(int j=0;j<C;j++){
arr[i][j]=(s[j]=='.'? 1:0);
}
}
for (int i=1;i<R;i++) {
for (int j=0;j<C;j++){
if (arr[i][j]) arr[i][j]+=arr[i-1][j];
}
histogram(arr[i]);
}
//for(int i=1;i<=6;i++)cout<<i<<"*"<<maxX[i]<<endl;
int Q;
cin>>Q;
while(Q--){
int a,b;
cin>>a>>b;
if(b<=maxX[a])cout<<"YES\n";
else cout<<"NO\n";
}
return 0;
}

풀이는 여기까지입니다. 대회 알고리즘을 접은 이유라는 글도 적었긴 했는데, 그럼에도 알고리즘은 도전할만한 가치가 충분하고 저희 학교의 학우 분들도 PS에 많은 관심이 생겼으면 좋겠습니다. 그러기에 이번 첫 교내 알고리즘 대회가 의미가 뜻깊습니다. 다시 한번 수고한 학생회와 출제진, 검수진 분들에게 박수 쳐주고 싶습니다. 고생 많으셨습니다.
내가 대회 알고리즘을 접은 이유
안녕하세요. 오랜만의 일상 글입니다. 최근 블로그에 개발 글만 올라와서 내가 봐도 재미가 없어 보이기도 하고 해서, 대회 알고리즘에 관해 제 생각을 조금 적어 두려 합니다. 우선 저는 대회
newdeal123.tistory.com
내년에는 졸업생이니, 기회가 된다면 출제진으로 만나 뵙겠습니다.
P.S. 알고리즘이나 개발에 관심 있어 저희 교내 학과 동아리인 NL 에 입부를 희망하시는 분은 비공개 댓글 달아주시길 바랍니다. 언제든 환영입니다..! ☺️
