https://www.acmicpc.net/problem/17940
17940번: 지하철
대학원생인 형욱이는 연구실에 출근할 때 주로 지하철을 이용한다. 지하철은 A와 B, 두 개의 회사에서 운영하고 있다. 두 회사는 경쟁사 관계로 사람들이 상대 회사의 지하철을 이용하는 것을 매우 싫어한다. 그래서 A와 B는 모두 상대 회사의 지하철로 환승할 때 마다 비싼 요금을 받고 있다. 형욱이는 가난한 대학원생이기 때문에 돈을 아끼는 것이 가장 중요하다. 형욱이에게 최적의 출근경로를 찾아주자. 최적의 출근 경로란 환승 횟수를 최소로 하는 경로 중 소요
www.acmicpc.net
문제
대학원생인 형욱이는 연구실에 출근할 때 주로 지하철을 이용한다. 지하철은 A와 B, 두 개의 회사에서 운영하고 있다. 두 회사는 경쟁사 관계로 사람들이 상대 회사의 지하철을 이용하는 것을 매우 싫어한다. 그래서 A와 B는 모두 상대 회사의 지하철로 환승할 때 마다 비싼 요금을 받고 있다.
형욱이는 가난한 대학원생이기 때문에 돈을 아끼는 것이 가장 중요하다. 형욱이에게 최적의 출근경로를 찾아주자. 최적의 출근 경로란 환승 횟수를 최소로 하는 경로 중 소요시간이 가장 짧은 경로이다. 여기에서의 환승은 이동하면서 지하철역을 운영하는 회사가 바뀔 때 마다 환승 1회로 계산한다.
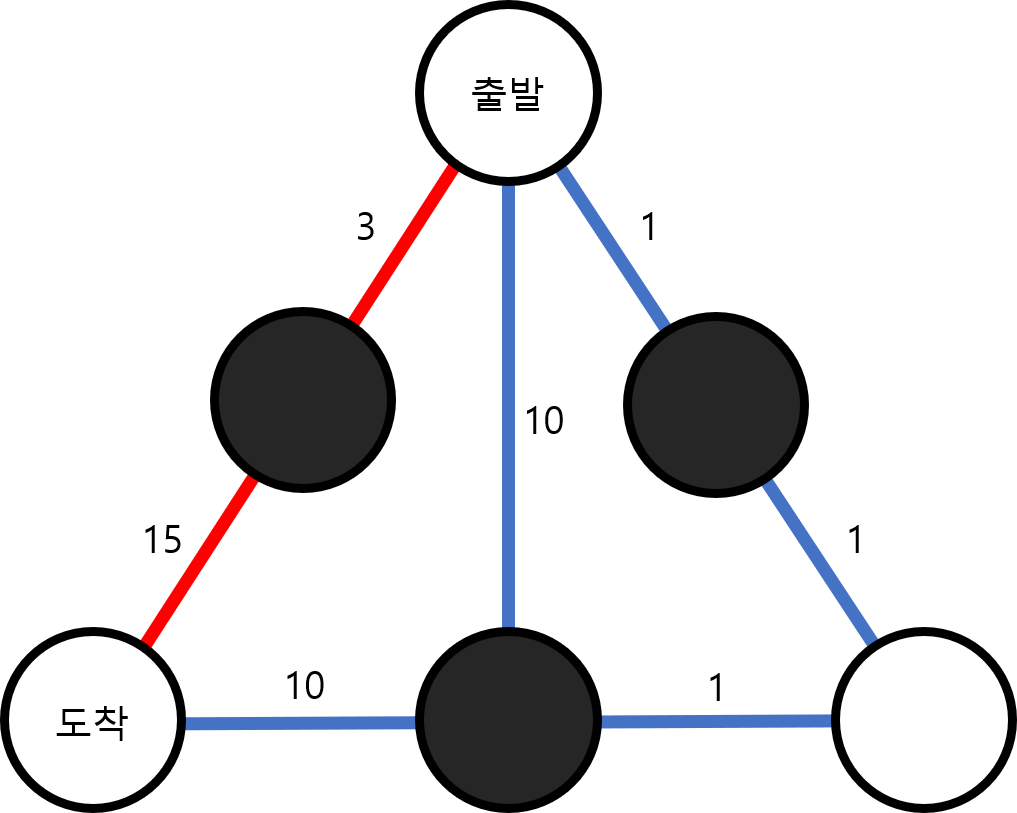
위의 그림에서 원은 지하철역을 의미하고 선들은 지하철역들이 연결되어 있는 지를 나타낸다. 흰색으로 표시된 지하철역은 A회사가 운영하는 지하철역이고 검은색으로 표시된 역은 B회사가 운영하는 지하철역이다. 이 때 붉게 표시된 경로로 이동하는 것이 환승 2회로 가장 적게 환승하면서 시간이 가장 짧은 경로이다.
입력
첫째 줄에 지하철역의 수 N과 도착지의 번호 M이 공백을 사이에 두고 정수로 주어진다. 지하철역은 순서대로 0 부터 N-1까지 존재하며 출발지는 항상 0 이다. (2 ≤ N ≤ 1000, 0 < M < 1000)
그 다음 N 줄에 걸쳐 각각의 지하철역을 운영하는 회사의 정보 Ci(0 ≤ i < N)가 0 또는 1로 주어진다. 0은 A회사를 뜻하고 1은 B회사를 뜻한다.
그 다음 N 줄은 지하철역간의 연결 상태 Eij(0 ≤ Eij ≤ 1000)가 정수로 주어진다. Eij가 0인 경우 i번째 역과 j번째 역이 연결되어 있지 않음을 의미하고 0보다 클 경우 두 역이 연결되어 있으며 요금이 Eij 만큼 듦을 의미한다.
출력
최적의 경로를 이용할 때 환승 횟수와 총 소요 시간을 공백으로 구분하여 출력한다.
또한 출발지와 도착지는 무조건 연결되어 있음이 보장된다.
좋은 디익스트라 연습문제라고 생각합니다. 디익스트라를 안짠지 오래되서 다시 공부하는데에 좋았습니다.
다른 기본적인 디익스트라 문제와 달리 특이하게, 요구하는 우선순위의 첫째가 최소환승이고, 소요시간은 그 다음입니다. 소요시간이 10이라도, 환승횟수가 2번이면 환승 1번에 시간10000보다 못하다는거죠. 일단 문제 푸는건 디익스트라 같긴한데.. 최소한승과 소요시간의 우선순위를 고려하는게 꽤 까다로울 것 같습니다. 그리고 이를 곧이 곧대로 구현하면
코딩이 까다로워집니다. 여기에 간단한 테크닉을 더하면 훨씬 문제를 쉽게 풀 수 있습니다. 우선 총 소요시간의 max값은 N*Eij의 최댓값이 분명합니다. 지하철이 일자로 쭉 이어져있는 형태를 상상하면 될 것같네요. 따라서 총 소요시간<10^6 임을 알 수 있습니다. 여기서 우리가 쓸 작은 테크닉은, 환승을 했을때에 임의로 10^6시간 만큼의 패널티를 부과하는 것 입니다. 총 소요시간은 10^6을 넘지않으니, 마지막에 디익스트라의 값에서 환승횟수와 소요시간을 구분하는건 쉽게 필터링 할 수 있습니다. 또한 환승횟수의 최댓값또한 N/2이므로(쭉 일자로 계속 환승을 했을 경우가 최대) 디익스트라값이 10^9를 넘지않습니다. 따라서 long long 을 쓰지 않고도 가볍게 디익스트라를 사용하면 됩니다.
#include <iostream>
#include <string.h>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int IMP=(int)1e6,INF=987654321;
int N,M;
vector<vector<pair<int,int>>>adj;
bool same_comp[1000+2];
int dijkstra()
{
vector<int>dis(N,INF);
dis[0]=0;
priority_queue<pair<int,int>>pq;
pq.push({0,0});
while(!pq.empty())
{
int cost=-pq.top().first,now=pq.top().second;
pq.pop();
if(cost>dis[now]) continue;
for(auto i:adj[now])
{
int next=i.first,nextDist=i.second+cost;
if(nextDist<dis[next])
{
dis[next]=nextDist;
pq.push({-nextDist,next});
}
}
}
return dis[M];
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin>>N>>M;
adj.resize(N);
for(int i=0;i<N;i++)cin>>same_comp[i];
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
int tmp;
cin>>tmp;
if(tmp)
{
if(same_comp[i]==same_comp[j])
adj[i].push_back({j,tmp});
else adj[i].push_back({j,tmp+IMP});
}
}
int ans=dijkstra();
cout<<ans/IMP<<" "<<ans%IMP;
}
if(tmp)절에서 환승여부를 검사해서 IMP를 더하는 부분만 제외하면, 일반적인 디익스트라 문제와 푸는 방법은
동일합니다. IMP값이 10의 제곱꼴이므로 디익스트라값에서 환승횟수와 소요시간을 분리하는 것은 ans/IMP와
ans%IMP로 쉽게 분리 할 수 있습니다.
'📌BOJ 알고리즘 트레이닝' 카테고리의 다른 글
| [BOJ][백준]dp-18118번 7-세그먼트 디스플레이 (0) | 2019.12.17 |
|---|---|
| [BOJ][백준]lazy propagation-17474번 수열과 쿼리 26 (0) | 2019.12.03 |
| [BOJ][백준]이분 매칭-18138번 리유나는 세일러복을 좋아해 (0) | 2019.11.28 |
| [BOJ][백준]BFS-17836번 공주님을 구해라! (0) | 2019.11.19 |
| [BOJ][백준]그리디 알고리즘-17609번 회문 (0) | 2019.11.15 |
https://www.acmicpc.net/problem/17940
17940번: 지하철
대학원생인 형욱이는 연구실에 출근할 때 주로 지하철을 이용한다. 지하철은 A와 B, 두 개의 회사에서 운영하고 있다. 두 회사는 경쟁사 관계로 사람들이 상대 회사의 지하철을 이용하는 것을 매우 싫어한다. 그래서 A와 B는 모두 상대 회사의 지하철로 환승할 때 마다 비싼 요금을 받고 있다. 형욱이는 가난한 대학원생이기 때문에 돈을 아끼는 것이 가장 중요하다. 형욱이에게 최적의 출근경로를 찾아주자. 최적의 출근 경로란 환승 횟수를 최소로 하는 경로 중 소요
www.acmicpc.net
문제
대학원생인 형욱이는 연구실에 출근할 때 주로 지하철을 이용한다. 지하철은 A와 B, 두 개의 회사에서 운영하고 있다. 두 회사는 경쟁사 관계로 사람들이 상대 회사의 지하철을 이용하는 것을 매우 싫어한다. 그래서 A와 B는 모두 상대 회사의 지하철로 환승할 때 마다 비싼 요금을 받고 있다.
형욱이는 가난한 대학원생이기 때문에 돈을 아끼는 것이 가장 중요하다. 형욱이에게 최적의 출근경로를 찾아주자. 최적의 출근 경로란 환승 횟수를 최소로 하는 경로 중 소요시간이 가장 짧은 경로이다. 여기에서의 환승은 이동하면서 지하철역을 운영하는 회사가 바뀔 때 마다 환승 1회로 계산한다.

위의 그림에서 원은 지하철역을 의미하고 선들은 지하철역들이 연결되어 있는 지를 나타낸다. 흰색으로 표시된 지하철역은 A회사가 운영하는 지하철역이고 검은색으로 표시된 역은 B회사가 운영하는 지하철역이다. 이 때 붉게 표시된 경로로 이동하는 것이 환승 2회로 가장 적게 환승하면서 시간이 가장 짧은 경로이다.
입력
첫째 줄에 지하철역의 수 N과 도착지의 번호 M이 공백을 사이에 두고 정수로 주어진다. 지하철역은 순서대로 0 부터 N-1까지 존재하며 출발지는 항상 0 이다. (2 ≤ N ≤ 1000, 0 < M < 1000)
그 다음 N 줄에 걸쳐 각각의 지하철역을 운영하는 회사의 정보 Ci(0 ≤ i < N)가 0 또는 1로 주어진다. 0은 A회사를 뜻하고 1은 B회사를 뜻한다.
그 다음 N 줄은 지하철역간의 연결 상태 Eij(0 ≤ Eij ≤ 1000)가 정수로 주어진다. Eij가 0인 경우 i번째 역과 j번째 역이 연결되어 있지 않음을 의미하고 0보다 클 경우 두 역이 연결되어 있으며 요금이 Eij 만큼 듦을 의미한다.
출력
최적의 경로를 이용할 때 환승 횟수와 총 소요 시간을 공백으로 구분하여 출력한다.
또한 출발지와 도착지는 무조건 연결되어 있음이 보장된다.
좋은 디익스트라 연습문제라고 생각합니다. 디익스트라를 안짠지 오래되서 다시 공부하는데에 좋았습니다.
다른 기본적인 디익스트라 문제와 달리 특이하게, 요구하는 우선순위의 첫째가 최소환승이고, 소요시간은 그 다음입니다. 소요시간이 10이라도, 환승횟수가 2번이면 환승 1번에 시간10000보다 못하다는거죠. 일단 문제 푸는건 디익스트라 같긴한데.. 최소한승과 소요시간의 우선순위를 고려하는게 꽤 까다로울 것 같습니다. 그리고 이를 곧이 곧대로 구현하면
코딩이 까다로워집니다. 여기에 간단한 테크닉을 더하면 훨씬 문제를 쉽게 풀 수 있습니다. 우선 총 소요시간의 max값은 N*Eij의 최댓값이 분명합니다. 지하철이 일자로 쭉 이어져있는 형태를 상상하면 될 것같네요. 따라서 총 소요시간<10^6 임을 알 수 있습니다. 여기서 우리가 쓸 작은 테크닉은, 환승을 했을때에 임의로 10^6시간 만큼의 패널티를 부과하는 것 입니다. 총 소요시간은 10^6을 넘지않으니, 마지막에 디익스트라의 값에서 환승횟수와 소요시간을 구분하는건 쉽게 필터링 할 수 있습니다. 또한 환승횟수의 최댓값또한 N/2이므로(쭉 일자로 계속 환승을 했을 경우가 최대) 디익스트라값이 10^9를 넘지않습니다. 따라서 long long 을 쓰지 않고도 가볍게 디익스트라를 사용하면 됩니다.
#include <iostream>
#include <string.h>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int IMP=(int)1e6,INF=987654321;
int N,M;
vector<vector<pair<int,int>>>adj;
bool same_comp[1000+2];
int dijkstra()
{
vector<int>dis(N,INF);
dis[0]=0;
priority_queue<pair<int,int>>pq;
pq.push({0,0});
while(!pq.empty())
{
int cost=-pq.top().first,now=pq.top().second;
pq.pop();
if(cost>dis[now]) continue;
for(auto i:adj[now])
{
int next=i.first,nextDist=i.second+cost;
if(nextDist<dis[next])
{
dis[next]=nextDist;
pq.push({-nextDist,next});
}
}
}
return dis[M];
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin>>N>>M;
adj.resize(N);
for(int i=0;i<N;i++)cin>>same_comp[i];
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
int tmp;
cin>>tmp;
if(tmp)
{
if(same_comp[i]==same_comp[j])
adj[i].push_back({j,tmp});
else adj[i].push_back({j,tmp+IMP});
}
}
int ans=dijkstra();
cout<<ans/IMP<<" "<<ans%IMP;
}
if(tmp)절에서 환승여부를 검사해서 IMP를 더하는 부분만 제외하면, 일반적인 디익스트라 문제와 푸는 방법은
동일합니다. IMP값이 10의 제곱꼴이므로 디익스트라값에서 환승횟수와 소요시간을 분리하는 것은 ans/IMP와
ans%IMP로 쉽게 분리 할 수 있습니다.
'📌BOJ 알고리즘 트레이닝' 카테고리의 다른 글
| [BOJ][백준]dp-18118번 7-세그먼트 디스플레이 (0) | 2019.12.17 |
|---|---|
| [BOJ][백준]lazy propagation-17474번 수열과 쿼리 26 (0) | 2019.12.03 |
| [BOJ][백준]이분 매칭-18138번 리유나는 세일러복을 좋아해 (0) | 2019.11.28 |
| [BOJ][백준]BFS-17836번 공주님을 구해라! (0) | 2019.11.19 |
| [BOJ][백준]그리디 알고리즘-17609번 회문 (0) | 2019.11.15 |
